题目内容
10.已知双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a>0,b>0)过点$(\sqrt{2},2\sqrt{2})$,过点(0,-2)的直线l与双曲线C的一条渐进线平行,且这两条平行线间的距离为$\frac{2}{3}$,则双曲线C的实轴长为( )| A. | 2 | B. | $2\sqrt{2}$ | C. | 4 | D. | $4\sqrt{2}$ |
分析 由双曲线的渐近线方程y=±$\frac{b}{a}$x,利用点到直线的距离公式,即可求得a和c的关系,即可求得b=2$\sqrt{2}$a,将点代入椭圆方程,即可求得a的值,求得双曲线C的实轴长.
解答 解:由双曲线的渐近线方程y=±$\frac{b}{a}$x,
则(0,-2)到渐近线bx-ay=0的距离d=$\frac{丨2a-0丨}{\sqrt{{a}^{2}+{b}^{2}}}$=$\frac{2a}{c}$=$\frac{2}{3}$,
则c=3a,即b=2$\sqrt{2}$a,
由双曲线C过点$(\sqrt{2},2\sqrt{2})$,
即$\frac{2}{{a}^{2}}-\frac{8}{8{a}^{2}}=1$,解得:a=1,
则双曲线C的实轴长为2a=2,
故选A.
点评 本题考查双曲线的简单几何性质,考查点到直线的距离公式,考查计算能力,属于中档题.

练习册系列答案
相关题目
20.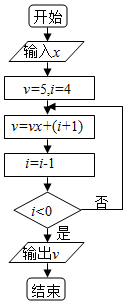 秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数学九章》中提出的多项式求值的秦九韶算法至今仍是比较先进的算法.如图的程序框图是针对某一多项式求值的算法,如果输入的x的值为2,则输出的v的值为( )
秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数学九章》中提出的多项式求值的秦九韶算法至今仍是比较先进的算法.如图的程序框图是针对某一多项式求值的算法,如果输入的x的值为2,则输出的v的值为( )
 秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数学九章》中提出的多项式求值的秦九韶算法至今仍是比较先进的算法.如图的程序框图是针对某一多项式求值的算法,如果输入的x的值为2,则输出的v的值为( )
秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数学九章》中提出的多项式求值的秦九韶算法至今仍是比较先进的算法.如图的程序框图是针对某一多项式求值的算法,如果输入的x的值为2,则输出的v的值为( )| A. | 129 | B. | 144 | C. | 258 | D. | 289 |
18.在平行四边形ABCD中,$|{\overrightarrow{AD}}|=3,|{\overrightarrow{AB}}|=5,\overrightarrow{AE}=\frac{2}{3}\overrightarrow{AD},\overrightarrow{BF}=\frac{1}{3}\overrightarrow{BC},cosA=\frac{3}{5}$,则$|{\overrightarrow{EF}}$|=( )
| A. | $\sqrt{14}$ | B. | $2\sqrt{5}$ | C. | $4\sqrt{2}$ | D. | $2\sqrt{11}$ |
5.已知点F2,P分别为双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的右焦点与右支上的一点,O为坐标原点,若点M是PF2的中点,$|{\overrightarrow{O{F_2}}}|=|{\overrightarrow{{F_2}M}}$|,且$\overrightarrow{O{F_2}}•\overrightarrow{{F_2}M}=\frac{c^2}{2}$,则该双曲线的离心率为( )
| A. | $\frac{{\sqrt{3}+1}}{2}$ | B. | $\frac{3}{2}$ | C. | $\sqrt{3}$ | D. | $2\sqrt{3}$ |
15.已知实数x,y满足条件$\left\{\begin{array}{l}x-y+3≥0\\ 2x+y-4≥0\\ x≤3\end{array}\right.$则z=x2+(y+1)2的最小值为5.
20.下列函数既是奇函数,又在区间[-1,1]上单调递减的是( )
| A. | f(x)=sinx | B. | f(x)=|x+1| | C. | f(x)=-x | D. | f(x)=cosx |