题目内容
14.若f(x)为奇函数,且x0是y=f(x)-ex的一个零点,则下列函数中,-x0一定是其零点的函数是( )| A. | y=f(-x)•e-x-1 | B. | y=f(x)•ex+1 | C. | y=f(x)•ex-1 | D. | y=f(-x)•ex+1 |
分析 根据题意,x0是y=f(x)-ex的一个零点,则有f(x0)=${e}^{{x}_{0}}$,结合函数的奇偶性依次分析选项,验证-x0是不是其零点,即可得答案.
解答 解:根据题意,x0是y=f(x)-ex的一个零点,则有f(x0)=${e}^{{x}_{0}}$,
依次分析选项:
对于A、y=f(-x)•e-x-1,将x=-x0代入可得:y=f(x0)${e}^{{x}_{0}}$-1≠0,不符合题意;
对于B、y=f(x)•ex+1,将x=-x0代入可得:y=f(-x0)${e}^{-{x}_{0}}$+1=-${e}^{{x}_{0}}$•${e}^{-{x}_{0}}$+1=0,即-x0一定是其零点,符合题意,
对于C、y=f(x)•ex-1,将x=-x0代入可得:y=f(-x0)${e}^{-{x}_{0}}$-1=-${e}^{{x}_{0}}$•${e}^{-{x}_{0}}$-1≠0,不符合题意;
对于D、y=f(-x)•ex+1,将x=-x0代入可得:y=f(x0)${e}^{-{x}_{0}}$+1=${e}^{{x}_{0}}$•${e}^{-{x}_{0}}$+1≠0,不符合题意;
故选:B.
点评 本题考查函数的零点的定义,涉及函数奇偶性的性质,关键是灵活运用函数的奇偶性性质.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
9.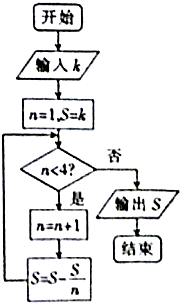 我国古代数学著作《九章算术》有如下问题:“今有器中米,不知其数,前人取半,中人三分取一,后人四分取一,余米一斗五升.问,米几何?”如图是解决该问题的程序框图,执行该程序框图,若输出的S=1.5(单位:升),则输入k的值为( )
我国古代数学著作《九章算术》有如下问题:“今有器中米,不知其数,前人取半,中人三分取一,后人四分取一,余米一斗五升.问,米几何?”如图是解决该问题的程序框图,执行该程序框图,若输出的S=1.5(单位:升),则输入k的值为( )
 我国古代数学著作《九章算术》有如下问题:“今有器中米,不知其数,前人取半,中人三分取一,后人四分取一,余米一斗五升.问,米几何?”如图是解决该问题的程序框图,执行该程序框图,若输出的S=1.5(单位:升),则输入k的值为( )
我国古代数学著作《九章算术》有如下问题:“今有器中米,不知其数,前人取半,中人三分取一,后人四分取一,余米一斗五升.问,米几何?”如图是解决该问题的程序框图,执行该程序框图,若输出的S=1.5(单位:升),则输入k的值为( )| A. | 4.5 | B. | 6 | C. | 7.5 | D. | 9 |
6.已知A={x|-4<x<1},B={x|x2-x-6<0},则A∪B等于( )
| A. | (-3,1) | B. | (-2,1) | C. | (-4,2) | D. | (-4,3) |
3.已知集合A={x|(x-6)(3x+8)<0},B={x|y=$\sqrt{x+1}$},则A∩B等于( )
| A. | [-1,6) | B. | (-1,6) | C. | (-$\frac{8}{3}$,-1] | D. | (-$\frac{8}{3}$,-1) |