1.若P为可行域$\left\{\begin{array}{l}x≥-1\\ y≤2\\ 2x-y+2≤0\end{array}\right.$内的一点,过P的直线l与圆O:x2+y2=7交于A,B两点,则|AB|的最小值为( )
| A. | $2\sqrt{3}$ | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | $2\sqrt{2}$ |
20.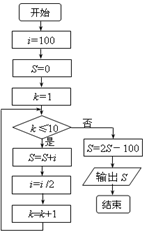 一个小球从100米高处自由落下,每次着地后又跳回到原高度的一半再落下.执行下面的程序框图,则输出的S表示的是( )
一个小球从100米高处自由落下,每次着地后又跳回到原高度的一半再落下.执行下面的程序框图,则输出的S表示的是( )
 一个小球从100米高处自由落下,每次着地后又跳回到原高度的一半再落下.执行下面的程序框图,则输出的S表示的是( )
一个小球从100米高处自由落下,每次着地后又跳回到原高度的一半再落下.执行下面的程序框图,则输出的S表示的是( )| A. | 小球第10次着地时向下的运动共经过的路程 | |
| B. | 小球第11次着地时向下的运动共经过的路程 | |
| C. | 小球第10次着地时一共经过的路程 | |
| D. | 小球第11次着地时一共经过的路程 |
19.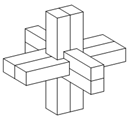 如图为中国传统智力玩具鲁班锁,起源于古代汉族建筑中首创的榫卯结构,这种三维的拼插器具内部的凹凸部分(即榫卯结构)啮合,外观看是严丝合缝的十字立方体,其上下、左右、前后完全对称,六根完全相同的正四棱柱分成三组,经90°榫卯起来.现有一鲁班锁的正四棱柱的底面正方形边长为1,欲将其放入球形容器内(容器壁的厚度忽略不计),若球形容器表面积的最小值为30π,则正四棱柱体的高为( )
如图为中国传统智力玩具鲁班锁,起源于古代汉族建筑中首创的榫卯结构,这种三维的拼插器具内部的凹凸部分(即榫卯结构)啮合,外观看是严丝合缝的十字立方体,其上下、左右、前后完全对称,六根完全相同的正四棱柱分成三组,经90°榫卯起来.现有一鲁班锁的正四棱柱的底面正方形边长为1,欲将其放入球形容器内(容器壁的厚度忽略不计),若球形容器表面积的最小值为30π,则正四棱柱体的高为( )
 如图为中国传统智力玩具鲁班锁,起源于古代汉族建筑中首创的榫卯结构,这种三维的拼插器具内部的凹凸部分(即榫卯结构)啮合,外观看是严丝合缝的十字立方体,其上下、左右、前后完全对称,六根完全相同的正四棱柱分成三组,经90°榫卯起来.现有一鲁班锁的正四棱柱的底面正方形边长为1,欲将其放入球形容器内(容器壁的厚度忽略不计),若球形容器表面积的最小值为30π,则正四棱柱体的高为( )
如图为中国传统智力玩具鲁班锁,起源于古代汉族建筑中首创的榫卯结构,这种三维的拼插器具内部的凹凸部分(即榫卯结构)啮合,外观看是严丝合缝的十字立方体,其上下、左右、前后完全对称,六根完全相同的正四棱柱分成三组,经90°榫卯起来.现有一鲁班锁的正四棱柱的底面正方形边长为1,欲将其放入球形容器内(容器壁的厚度忽略不计),若球形容器表面积的最小值为30π,则正四棱柱体的高为( )| A. | $2\sqrt{6}$ | B. | $2\sqrt{7}$ | C. | $4\sqrt{2}$ | D. | 5 |
18.已知函数$f(x)=\left\{\begin{array}{l}{2^{1-|x|}},x≤1\\-{(x-2)^2},x>1\end{array}\right.$,若$f(m)=\frac{1}{4}$,则f(1-m)=( )
| A. | -1 | B. | -4 | C. | -9 | D. | -16 |
17.为了得到函数y=cos2x的图象,只要把函数$y=sin(2x-\frac{π}{3})$的图象上所有的点( )
| A. | 向右平行移动$\frac{5π}{12}$个单位长度 | B. | 向左平行移动$\frac{5π}{12}$个单位长度 | ||
| C. | 向右平行移动$\frac{5π}{6}$个单位长度 | D. | 向左平行移动$\frac{5π}{6}$个单位长度 |
16.在数列{an}中,a1=2,an+1=an+2,Sn为{an}的前n项和,则S10=( )
| A. | 90 | B. | 100 | C. | 110 | D. | 130 |
15.复数$z=\frac{-1+i}{2-i}$的虚部为( )
0 239081 239089 239095 239099 239105 239107 239111 239117 239119 239125 239131 239135 239137 239141 239147 239149 239155 239159 239161 239165 239167 239171 239173 239175 239176 239177 239179 239180 239181 239183 239185 239189 239191 239195 239197 239201 239207 239209 239215 239219 239221 239225 239231 239237 239239 239245 239249 239251 239257 239261 239267 239275 266669
| A. | $-\frac{3}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{1}{5}$ | D. | $-\frac{1}{5}$ |