题目内容

18．已知函数$f（x）=\left\{\begin{array}{l}{2^{1-|x|}}，x≤1\\-{（x-2）^2}，x＞1\end{array}\right.$，若$f（m）=\frac{1}{4}$，则f（1-m）=（　　）
A．-1B．-4C．-9D．-16

分析 由分段函数解析式结合f（m）=$\frac{1}{4}$可知m≤1，把x=m代入函数解析式求得m值，则f（1-m）可求．

解答 解：由题意可知，m≤1，
∴f（m）=${2}^{1-|m|}=\frac{1}{4}={2}^{-2}$，
∴1-|m|=-2，解得m=3（舍）或m=-3．
则f（1-m）=f（4）=-（4-2）2=-4．
故选：B．

点评 本题考查函数值的求法，考查分段函数的应用，是基础的计算题．

练习册系列答案
相关题目
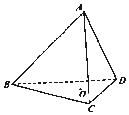8．如图，在正四面体ABCD中，O是△BCD的中心，E，F分别是AB，AC上的动点，且$\overrightarrow{BE}$=λ$\overrightarrow{BA}$，$\overrightarrow{CF}$=（1-λ）$\overrightarrow{CA}$
（1）若OE∥平面ACD，求实数λ的值；
（2）若λ=$\frac{1}{2}$，正四面体ABCD的棱长为2$\sqrt{2}$，求平面DEF和平面BCD所成的角余弦值．
9．甲盒子中有编号分别为1，2的两个乒乓球，乙盒子中有编号分别为3，4，5，6的四个乒乓球．现分别从两个盒子中随机地各取出1个乒乓球，则取出的乒乓球的编号之和大于6的概率为$\frac{3}{8}$．
6．已知向量$\overrightarrow{a}$，$\overrightarrow{b}$满足$\overrightarrow{a}$•$\overrightarrow{b}$=2，且$\overrightarrow{b}$=（1，$\sqrt{3}$），则$\overrightarrow{a}$+$\overrightarrow{b}$在$\overrightarrow{b}$方向上的投影为3．
13．在直角坐标系xOy中，已知点P（2，0），曲线C的参数方程为$\left\{\begin{array}{l}x=4{t^2}\\ y=4t\end{array}\right.$（t为参数）．以坐标原点为极点，x轴正半轴为极轴建立极坐标系．
（Ⅰ）求曲线C的普通方程和极坐标方程；
（Ⅱ）过点P且倾斜角为$\frac{π}{4}$的直线l交曲线C于A，B两点，求|AB|．
3．设向量$\overrightarrow{AB}=（x，x+1），\overrightarrow{CD}=（1，-2）$，且$\overrightarrow{AB}$∥$\overrightarrow{CD}$，则x=-$\frac{1}{3}$．
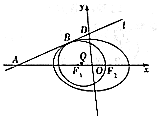4．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左、右焦点分别为F1、F2，过点A（-4，0）的直线l与椭圆C相切于点B，与y轴交于点D（0，2），又椭圆的离心率为$\frac{1}{2}$．
（1）求椭圆C的方程；
（2）圆Q与直线l相切于点B，且经过点F2，求圆Q的方程，并判断圆Q与圆x2+y2=a2的位置关系．
1．已知非零向量$\overrightarrow{a}$，$\overrightarrow{b}$满足$\overrightarrow{a}$•$\overrightarrow{b}$=0，|$\overrightarrow{a}$|=3，且$\overrightarrow{a}$与$\overrightarrow{a}$+$\overrightarrow{b}$的夹角为$\frac{π}{4}$，则|$\overrightarrow{b}$|=（　　）
A．6B．3$\sqrt{2}$C．2$\sqrt{2}$D．3
2．已知a，b，c为正实数，求证：$\frac{b^2}{a}+\frac{c^2}{b}+\frac{a^2}{c}≥a+b+c$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网