题目内容
13.在直角坐标系xOy中,已知点P(2,0),曲线C的参数方程为$\left\{\begin{array}{l}x=4{t^2}\\ y=4t\end{array}\right.$(t为参数).以坐标原点为极点,x轴正半轴为极轴建立极坐标系.(Ⅰ)求曲线C的普通方程和极坐标方程;
(Ⅱ)过点P且倾斜角为$\frac{π}{4}$的直线l交曲线C于A,B两点,求|AB|.
分析 (Ⅰ)利用三种方程的转化方法,即可求曲线C的普通方程和极坐标方程;
(Ⅱ)直线l的标准参数方程为$\left\{\begin{array}{l}x=2+\frac{{\sqrt{2}}}{2}s\\ y=\frac{{\sqrt{2}}}{2}s\end{array}\right.(s为参数)$,将其代入y2=4x,利用参数的几何意义,即可求|AB|.
解答 解:(Ⅰ)因为$\left\{\begin{array}{l}x=4{t^2}\\ y=4t\end{array}\right.$消t得曲线C的普通方程为y2=4x.(2分)
∵x=ρcosθ,y=ρsinθ,∴ρ2sin2θ=4ρcosθ,
即曲线C的极坐标方程为ρsin2θ=4cosθ.(5分)
(Ⅱ)因为直线l过点P(2,0)且倾斜角为$\frac{π}{4}$,
所以直线l的标准参数方程为$\left\{\begin{array}{l}x=2+\frac{{\sqrt{2}}}{2}s\\ y=\frac{{\sqrt{2}}}{2}s\end{array}\right.(s为参数)$,(7分)
将其代入y2=4x,整理可得${s^2}-4\sqrt{2}s-16=0$,(8分)$△={(-4\sqrt{2})^2}+4×16>0$,
设A,B对应的参数分别为s1,s2则 ${s_1}+{s_2}=4\sqrt{2},{s_1}{s_2}=-16$,
所以$|{AB}|=|{{s_1}-{s_2}}|=\sqrt{{{({s_1}+{s_2})}^2}-4{s_1}{s_2}}=\sqrt{{{(4\sqrt{2})}^2}+4×16}=4\sqrt{6}$.(10分)
点评 本题考查三种方程的转化,考查参数方程的运用,考查参数的几何意义,属于中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | $\frac{{\overrightarrow{a}}^{2}-{\overrightarrow{b}}^{2}}{|\overrightarrow{a}|}$ | B. | $\frac{{\overrightarrow{a}}^{2}-{\overrightarrow{b}}^{2}}{{\overrightarrow{a}}^{2}}$ | C. | $\frac{{\overrightarrow{b}}^{2}-{\overrightarrow{a}}^{2}}{|\overrightarrow{b}|}$ | D. | $\frac{{\overrightarrow{a}}^{2}-{\overrightarrow{b}}^{2}}{|\overrightarrow{b}|}$ |
| A. | -1 | B. | -4 | C. | -9 | D. | -16 |
(I)求雕刻师当天收入(单位:元)关于雕刻量n(单位:粒,n∈N)的函数解析式f(n);
(Ⅱ)该雕刻师记录了过去10天每天的雕刻量n(单位:粒),整理得如表:
| 雕刻量n | 210 | 230 | 250 | 270 | 300 |
| 频数 | 1 | 2 | 3 | 3 | 1 |
(ⅰ)求该雕刻师这10天的平均收入;
(ⅱ)求该雕刻师当天收入不低于300元的概率.
| A. | (2kπ+$\frac{π}{6}$,2kπ+$\frac{5π}{6}$),k∈Z | |
| B. | (2kπ-$\frac{π}{6}$,2kπ)∪(2kπ,2kπ+π)∪(2kπ+π,2kπ+$\frac{7}{6}$π),k∈Z | |
| C. | (2kπ-$\frac{5π}{6}$,2kπ-$\frac{π}{6}$),k∈Z | |
| D. | (2kπ-$\frac{7π}{6}$,2kπ-π)∪(2kπ-π,2kπ)∪(2kπ,2kπ+$\frac{π}{6}$),k∈Z |
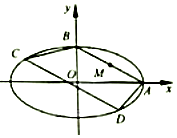 如图,在平面直角坐标系xoy中,椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的右顶点和上顶点分别为点A,B,M是线段AB的中点,且$\overrightarrow{OM}•\overrightarrow{AB}=-\frac{3}{2}{b^2}$..
如图,在平面直角坐标系xoy中,椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的右顶点和上顶点分别为点A,B,M是线段AB的中点,且$\overrightarrow{OM}•\overrightarrow{AB}=-\frac{3}{2}{b^2}$..