题目内容
1.若P为可行域$\left\{\begin{array}{l}x≥-1\\ y≤2\\ 2x-y+2≤0\end{array}\right.$内的一点,过P的直线l与圆O:x2+y2=7交于A,B两点,则|AB|的最小值为( )| A. | $2\sqrt{3}$ | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | $2\sqrt{2}$ |
分析 由约束条件作出可行域,求出可行域内到原点距离最远的点,然后结合弦心距、圆的半径及弦长间的关系得答案.
解答 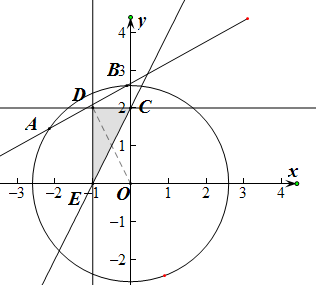 解:不等式可行域$\left\{\begin{array}{l}x≥-1\\ y≤2\\ 2x-y+2≤0\end{array}\right.$如图所示
解:不等式可行域$\left\{\begin{array}{l}x≥-1\\ y≤2\\ 2x-y+2≤0\end{array}\right.$如图所示
联立$\left\{\begin{array}{l}{x=-1}\\{y=2}\end{array}\right.$,解得D(-1,2).
由图可知,可行域内的点中,D 到原点的距离最大,为$\sqrt{5}$,
∴|AB|的最小值为2$\sqrt{7-5}$=2$\sqrt{2}$
故选:D
点评 本题考查简单的线性规划,考查了数形结合的解题思想方法,训练了直线与圆位置关系的应用,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.漳州水仙鳞茎硕大,箭多花繁,色美香郁,素雅娟丽,有“天下水仙数漳州”之美誉.现某水仙花雕刻师受雇每天雕刻250粒水仙花,雕刻师每雕刻一粒可赚1.2元,如果雕刻师当天超额完成任务,则超出的部分每粒多赚0.5元;如果当天未能按量完成任务,则按完成的雕刻量领取当天工资.
(Ⅰ)求雕刻师当天收入(单位:元)关于雕刻量n(单位:粒,n∈N)的函数解析式f(n);
(Ⅱ)该雕刻师记录了过去10天每天的雕刻量n(单位:粒),整理得如表:
以10天记录的各雕刻量的频率作为各雕刻量发生的概率.
(ⅰ)在当天的收入不低于276元的条件下,求当天雕刻量不低于270个的概率;
(ⅱ)若X表示雕刻师当天的收入(单位:元),求X的分布列和数学期望.
(Ⅰ)求雕刻师当天收入(单位:元)关于雕刻量n(单位:粒,n∈N)的函数解析式f(n);
(Ⅱ)该雕刻师记录了过去10天每天的雕刻量n(单位:粒),整理得如表:
| 雕刻量n | 210 | 230 | 250 | 270 | 300 |
| 频数 | 1 | 2 | 3 | 3 | 1 |
(ⅰ)在当天的收入不低于276元的条件下,求当天雕刻量不低于270个的概率;
(ⅱ)若X表示雕刻师当天的收入(单位:元),求X的分布列和数学期望.
16.在数列{an}中,a1=2,an+1=an+2,Sn为{an}的前n项和,则S10=( )
| A. | 90 | B. | 100 | C. | 110 | D. | 130 |
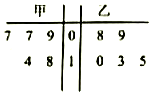 如图是甲、乙两名篮球运动员在五场比赛中所得分数的茎叶图,则在这五场比赛中得分较为稳定(方差较小)的那名运动员的得分的方差为$\frac{34}{5}$.
如图是甲、乙两名篮球运动员在五场比赛中所得分数的茎叶图,则在这五场比赛中得分较为稳定(方差较小)的那名运动员的得分的方差为$\frac{34}{5}$.