15．我们知道：“平面中到定点等于定长的点轨迹是圆”拓展至空间：“空间中到定点的距离等于定长的点的轨迹是球”，类似可得：已知A（-1，0，0），B（1，0，0），则点集{P（x，y，z）||PA|-|PB|=1}在空间中的轨迹描述正确的是（ ）
| A． | 以A，B为焦点的双曲线绕轴旋转而成的旋转曲面 | |
| B． | 以A，B为焦点的椭球体 | |
| C． | 以A，B为焦点的双曲线单支绕轴旋转而成的旋转曲面 | |
| D． | 以上都不对 |
14．“Z=$\frac{1}{sinθ+cosθ•i}$-$\frac{1}{2}$（其中i是虚数单位）是纯虚数．”是“θ=$\frac{π}{6}$+2kπ”的（ ）条件．
| A． | 充分不必要 | B． | 必要不充分 | ||
| C． | 充要 | D． | 既不充分也不必要 |
13．设集合A={x|$\frac{2}{x-1}$≥1}，B={y|y=log2x，0＜x≤4}，则A∩B=（ ）
| A． | ∅ | B． | （1，2] | C． | （-∞，1） | D． | [2，3] |
12．《九章算术》卷第六《均输》中，有问题“今有竹九节，下三节容量四升，上四节容量三升．问中间二节欲均容，各多少？”其中“欲均容”的意思是：使容量变化均匀，即由下往上均匀变细．在这个问题中的中间两节容量和是（ ）
| A． | $1\frac{61}{66}$升 | B． | 2升 | C． | $2\frac{3}{22}$升 | D． | 3升 |
11．已知直线m，n与平面α，β，γ满足α⊥β，α∩β=m，n⊥α，n?γ，则下列判断一定正确的是（ ）
| A． | m∥γ，α⊥γ | B． | n∥β，α⊥γ | C． | β∥γ，α⊥γ | D． | m⊥n，α⊥γ |
10．已知等腰梯形ABCD中AB∥CD，AB=2CD=4，∠BAD=60°，双曲线以A，B为焦点，且经过C，D两点，则该双曲线的离心率等于（ ）
| A． | $\sqrt{2}$ | B． | $\sqrt{3}$ | C． | $\sqrt{5}$ | D． | $\sqrt{3}+1$ |
9．已知函数f（x）=sinx-x，则不等式f（x+2）+f（1-2x）＜0的解集是（ ）
| A． | $（-∞，-\frac{1}{3}）$ | B． | $（-\frac{1}{3}，+∞）$ | C． | （3，+∞） | D． | （-∞，3） |
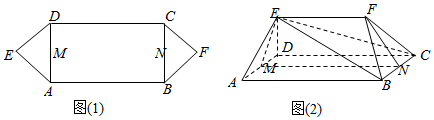
8．执行如图程序框图，输出的S为（ ）
0 239017 239025 239031 239035 239041 239043 239047 239053 239055 239061 239067 239071 239073 239077 239083 239085 239091 239095 239097 239101 239103 239107 239109 239111 239112 239113 239115 239116 239117 239119 239121 239125 239127 239131 239133 239137 239143 239145 239151 239155 239157 239161 239167 239173 239175 239181 239185 239187 239193 239197 239203 239211 266669
| A． | $\frac{1}{7}$ | B． | $\frac{2}{7}$ | C． | $\frac{4}{7}$ | D． | $\frac{6}{7}$ |
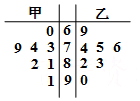某人到甲、乙两市各7个小区调查空置房情况，调查得到的小区空置房的套数绘成了如图的茎叶图，则调查中甲市空置房套数的中位数与乙市空置房套数的中位数之差为（ ）