题目内容
10.已知等腰梯形ABCD中AB∥CD,AB=2CD=4,∠BAD=60°,双曲线以A,B为焦点,且经过C,D两点,则该双曲线的离心率等于( )| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{5}$ | D. | $\sqrt{3}+1$ |
分析 利用双曲线的简单性质,直接列出关系式求解双曲线的离心率即可.
解答 解:等腰梯形ABCD中AB∥CD,AB=2CD=4,∠BAD=60°,双曲线以A,B为焦点,且经过C,D两点,
双曲线过点C时,$e=\frac{c}{a}=\frac{AB}{CA-CB}=\sqrt{3}+1$,
故选:D.
点评 本题考查双曲线的简单性质的应用,离心率的求法,考查计算能力.

练习册系列答案
相关题目
1.若$\frac{a+i}{1+2i}=ti$(i为虚数单位,a,t∈R),则t+a等于( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
18. 如图,“赵爽弦图”是由四个全等的直角三角形(阴影部分)围成一个大正方形,中间空出一个小正方形组成的图形,若在大正方形内随机取一点,该点落在小正方形的概率为$\frac{1}{5}$,则图中直角三角形中较大锐角的正弦值为( )
如图,“赵爽弦图”是由四个全等的直角三角形(阴影部分)围成一个大正方形,中间空出一个小正方形组成的图形,若在大正方形内随机取一点,该点落在小正方形的概率为$\frac{1}{5}$,则图中直角三角形中较大锐角的正弦值为( )
 如图,“赵爽弦图”是由四个全等的直角三角形(阴影部分)围成一个大正方形,中间空出一个小正方形组成的图形,若在大正方形内随机取一点,该点落在小正方形的概率为$\frac{1}{5}$,则图中直角三角形中较大锐角的正弦值为( )
如图,“赵爽弦图”是由四个全等的直角三角形(阴影部分)围成一个大正方形,中间空出一个小正方形组成的图形,若在大正方形内随机取一点,该点落在小正方形的概率为$\frac{1}{5}$,则图中直角三角形中较大锐角的正弦值为( )| A. | $\frac{\sqrt{5}}{5}$ | B. | $\frac{2\sqrt{5}}{5}$ | C. | $\frac{1}{5}$ | D. | $\frac{\sqrt{3}}{3}$ |
5.已知f(x)=x2•ex,若函数g(x)=f2(x)-kf(x)+1恰有三个零点,则下列结论正确的是( )
| A. | k=±2 | B. | k=$\frac{8}{{e}^{2}}$ | C. | k=2 | D. | k=$\frac{4}{{e}^{2}}$+$\frac{{e}^{2}}{4}$ |
15.我们知道:“平面中到定点等于定长的点轨迹是圆”拓展至空间:“空间中到定点的距离等于定长的点的轨迹是球”,类似可得:已知A(-1,0,0),B(1,0,0),则点集{P(x,y,z)||PA|-|PB|=1}在空间中的轨迹描述正确的是( )
| A. | 以A,B为焦点的双曲线绕轴旋转而成的旋转曲面 | |
| B. | 以A,B为焦点的椭球体 | |
| C. | 以A,B为焦点的双曲线单支绕轴旋转而成的旋转曲面 | |
| D. | 以上都不对 |
20.为调查我市居民对“文明出行”相关规定的了解情况,某媒体随机选取了30名行人进行问卷调查,将他们的年龄整理后分组,制成下表:
己知从中任选一人,年龄在(12,22]的频率为0.3
(I)求m,n的值;
(II)通过问卷得知,参与调查的52岁以上的两个组中,了解相关规定的人各占$\frac{1}{2}$.现从这两个组中任选2人,求选取的2人都了解相关规定的概率.
| 年龄(岁) | (12,22] | (22,32] | (32,42] | (42,52] | (52,62] | (62,72] |
| 频数 | m | 3 | 7 | 5 | 4 | n |
(I)求m,n的值;
(II)通过问卷得知,参与调查的52岁以上的两个组中,了解相关规定的人各占$\frac{1}{2}$.现从这两个组中任选2人,求选取的2人都了解相关规定的概率.
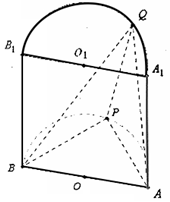 如图半圆柱OO1的底面半径和高都是1,面ABB1A1是它的轴截面(过上下底面圆心连线OO1的平面),Q,P分别是上下底面半圆周上一点.
如图半圆柱OO1的底面半径和高都是1,面ABB1A1是它的轴截面(过上下底面圆心连线OO1的平面),Q,P分别是上下底面半圆周上一点.