题目内容
9.已知函数f(x)=sinx-x,则不等式f(x+2)+f(1-2x)<0的解集是( )| A. | $(-∞,-\frac{1}{3})$ | B. | $(-\frac{1}{3},+∞)$ | C. | (3,+∞) | D. | (-∞,3) |
分析 根据题意,由函数奇偶性的定义分析可得函数f(x)是定义在R上的奇函数,对f(x)求导可得f'(x)=cosx-1≤0,即可得f(x)=sinx-x是减函数,则不等式f(x+2)+f(1-2x)<0可以转化为x+2>2x-1,解可得x的范围,即可得答案.
解答 解:函数f(x)=sinx-x,其定义域为R,且f(-x)=sin(-x)-(-x)=-(sinx-x),
则函数f(x)是定义在R上的奇函数,
导函数是f'(x)=cosx-1≤0,所以f(x)=sinx-x是减函数,
不等式f(x+2)+f(1-2x)<0⇒f(x+2)<f(2x-1),
即x+2>2x-1⇒x<3,
故选:D.
点评 本题考查函数奇偶性与单调性的综合应用,关键是分析函数f(x)的奇偶性与单调性.

练习册系列答案
相关题目
20.已知集合A={x|y=lg(3-2x)},B={x|x2≤4},则A∪B=( )
| A. | $\{\left.x\right|-2≤x<\frac{3}{2}\}$ | B. | {x|x<2} | C. | $\{\left.x\right|-2<x<\frac{3}{2}\}$ | D. | {x|x≤2} |
4.已知实数x,y满足条件$\left\{\begin{array}{l}{3x+y-7≥0}\\{x+3y-13≤0}\\{x-y-1≤0}\end{array}\right.$,则z=|2x+y|的最小值为( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
14.“Z=$\frac{1}{sinθ+cosθ•i}$-$\frac{1}{2}$(其中i是虚数单位)是纯虚数.”是“θ=$\frac{π}{6}$+2kπ”的( )条件.
| A. | 充分不必要 | B. | 必要不充分 | ||
| C. | 充要 | D. | 既不充分也不必要 |
18.若等比数列{an}的公比为q,则关于x,y的二元一次方程组$\left\{\begin{array}{l}{a_1}x+{a_3}y=2\\{a_2}x+{a_4}y=1\end{array}\right.$的解的情况下列说法正确的是( )
| A. | 对任意q∈R(q≠0),方程组都有唯一解 | |
| B. | 对任意q∈R(q≠0),方程组都无解 | |
| C. | 当且仅当$q=\frac{1}{2}$时,方程组有无穷多解 | |
| D. | 当且仅当$q=\frac{1}{2}$时,方程组无解 |
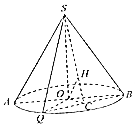 如图,圆锥的横截面为等边三角形SAB,O为底面圆圆心,Q为底面圆周上一点.
如图,圆锥的横截面为等边三角形SAB,O为底面圆圆心,Q为底面圆周上一点.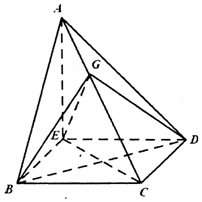 如图,在三棱锥A-BCD中,∠ABC=∠BCD=∠CDA=90°,AC=6$\sqrt{3}$,BC=CD=6,E点在平面BCD内,EC=BD,EC⊥BD.
如图,在三棱锥A-BCD中,∠ABC=∠BCD=∠CDA=90°,AC=6$\sqrt{3}$,BC=CD=6,E点在平面BCD内,EC=BD,EC⊥BD.