题目内容
14.“Z=$\frac{1}{sinθ+cosθ•i}$-$\frac{1}{2}$(其中i是虚数单位)是纯虚数.”是“θ=$\frac{π}{6}$+2kπ”的( )条件.| A. | 充分不必要 | B. | 必要不充分 | ||
| C. | 充要 | D. | 既不充分也不必要 |
分析 Z=$\frac{1}{sinθ+cosθ•i}$-$\frac{1}{2}$=sinθ$-\frac{1}{2}$-icosθ(其中i是虚数单位)是纯虚数.可得sinθ$-\frac{1}{2}$=0,cosθ≠0,解出θ即可判断出结论.
解答 解:Z=$\frac{1}{sinθ+cosθ•i}$-$\frac{1}{2}$=sinθ$-\frac{1}{2}$-icosθ(其中i是虚数单位)是纯虚数.
则sinθ$-\frac{1}{2}$=0,cosθ≠0,
解得:θ=2kπ+$\frac{π}{6}$或θ=2kπ+π+$\frac{π}{6}$(k∈Z).
∴Z=$\frac{1}{sinθ+cosθ•i}$-$\frac{1}{2}$(其中i是虚数单位)是纯虚数.”是“θ=$\frac{π}{6}$+2kπ”的必要不充分条件.
故选:B.
点评 本题考查了复数的运算法则、三角函数求值、简易逻辑的判定方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
4.已知等差数列{an}为各项均为正数,其前n项和为Sn,若a1=1,$\sqrt{{S}_{3}}$=a2,则a8=( )
| A. | 12 | B. | 13 | C. | 14 | D. | 15 |
5.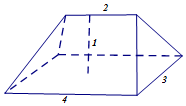 《九章算术》卷第五《商功》中,有问题“今有刍甍,下广三丈,袤四丈,上袤二丈,无广,高一丈.问积几何?”,意思是:“今有底面为矩形的屋脊状的楔体,下底面宽3丈,长4丈;上棱长2丈,无宽,高1丈(如图).
《九章算术》卷第五《商功》中,有问题“今有刍甍,下广三丈,袤四丈,上袤二丈,无广,高一丈.问积几何?”,意思是:“今有底面为矩形的屋脊状的楔体,下底面宽3丈,长4丈;上棱长2丈,无宽,高1丈(如图).
问它的体积是多少?”这个问题的答案是( )
 《九章算术》卷第五《商功》中,有问题“今有刍甍,下广三丈,袤四丈,上袤二丈,无广,高一丈.问积几何?”,意思是:“今有底面为矩形的屋脊状的楔体,下底面宽3丈,长4丈;上棱长2丈,无宽,高1丈(如图).
《九章算术》卷第五《商功》中,有问题“今有刍甍,下广三丈,袤四丈,上袤二丈,无广,高一丈.问积几何?”,意思是:“今有底面为矩形的屋脊状的楔体,下底面宽3丈,长4丈;上棱长2丈,无宽,高1丈(如图).问它的体积是多少?”这个问题的答案是( )
| A. | 5立方丈 | B. | 6立方丈 | C. | 7立方丈 | D. | 9立方丈 |
2.已知A={1,2,4},B={y|y=log2x,x∈A},则A∪B=( )
| A. | {1,2} | B. | [1,2] | C. | {0,1,2,4} | D. | [0,4] |
9.已知函数f(x)=sinx-x,则不等式f(x+2)+f(1-2x)<0的解集是( )
| A. | $(-∞,-\frac{1}{3})$ | B. | $(-\frac{1}{3},+∞)$ | C. | (3,+∞) | D. | (-∞,3) |
6.双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)离心率为$\sqrt{3}$,左右焦点分别为F1,F2,P为双曲线右支上一点,∠F1PF2的平分线为l,点F1关于l的对称点为Q,|F2Q|=2,则双曲线方程为( )
| A. | $\frac{{x}^{2}}{2}$-y2=1 | B. | x2-$\frac{{y}^{2}}{2}$=1 | C. | x2-$\frac{{y}^{2}}{3}$=1 | D. | $\frac{{x}^{2}}{3}$-y2=1 |
3.给出计算$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+…+$\frac{1}{2018}$的值的一个程序框图如图,其中判断框内应填入的条件是( )
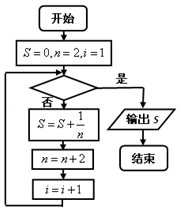

| A. | i>1009? | B. | i<1009? | C. | i>2018? | D. | i<2018? |
4.定义在R上的函数f(x)满足f(x+4)=f(x),f(x)=$\left\{\begin{array}{l}-{x^2}+1,\;\;-1≤x≤1\\-|{x-2}|+1,\;1<x≤3\end{array}$.若关于x的方程f(x)-ax=0有5个不同实根,则正实数a的取值范围是( )
| A. | $({\frac{1}{4},\frac{1}{3}})$ | B. | $({\frac{1}{6},\frac{1}{4}})$ | C. | $({16-6\sqrt{7},\frac{1}{6}})$ | D. | $({\frac{1}{6},8-2\sqrt{15}})$ |