题目内容
11.已知直线m,n与平面α,β,γ满足α⊥β,α∩β=m,n⊥α,n?γ,则下列判断一定正确的是( )| A. | m∥γ,α⊥γ | B. | n∥β,α⊥γ | C. | β∥γ,α⊥γ | D. | m⊥n,α⊥γ |
分析 对4个选项分别进行判断,即可得出结论.
解答 解:对于A选项中的直线m与平面γ的位置关系无法判断,不正确,
B选项中的直线n也可能落在平面β内,不正确;
C选项中的平面β与平面β也可能相交,不正确
D选项,因为n⊥α,n?γ,则α⊥γ;同时n⊥α,m?α,则m⊥n,所以D选项是正确的,
故选D.
点评 本题考查线面平行、平面与平面垂直、线面垂直的性质,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
2.已知随机变量ξ服从正态分布N(μ,σ2),若P(ξ<2)=P(ξ>6)=0.15,则P(2≤ξ<4)等于( )
| A. | 0.3 | B. | 0.35 | C. | 0.5 | D. | 0.7 |
19.执行如图的程序框图,则输出的S=( )
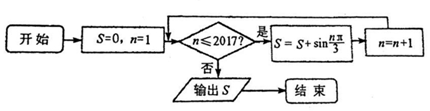

| A. | $\frac{\sqrt{3}}{2}$ | B. | $\sqrt{3}$ | C. | -$\frac{\sqrt{3}}{2}$ | D. | 0 |
16.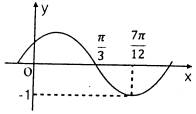 函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的图象如图所示,则下列有关f(x)性质的描述正确的是( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的图象如图所示,则下列有关f(x)性质的描述正确的是( )
 函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的图象如图所示,则下列有关f(x)性质的描述正确的是( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的图象如图所示,则下列有关f(x)性质的描述正确的是( )| A. | φ=$\frac{2π}{3}$ | B. | x=$\frac{7π}{12}$+kπ,k∈Z为其所有对称轴 | ||
| C. | [$\frac{π}{12}$+$\frac{kπ}{2}$,$\frac{7π}{12}$+$\frac{kπ}{2}$],k∈Z为其减区间 | D. | f(x)向左移$\frac{π}{12}$可变为偶函数 |
3. 鹰潭市龙虎山花语世界位于中国第八处世界自然遗产,世界地质公元、国家自然文化双遗产地、国家AAAAA级旅游景区--龙虎山主景区排衙峰下,是一座独具现代园艺风格的花卉公园,园内汇集了3000余种花卉苗木,一年四季姹紫嫣红花香四溢.花园景观融合法、英、意、美、日、中六大经典园林风格,景观设计唯美新颖.玫瑰花园、香草花溪、台地花海、植物迷宫、儿童乐园等景点错落有致,交相呼应又自成一体,是世界园艺景观的大展示.该景区自2015年春建成试运行以来,每天游人如织,郁金香、向日葵、虞美人等赏花旺季日入园人数最高达万人.
鹰潭市龙虎山花语世界位于中国第八处世界自然遗产,世界地质公元、国家自然文化双遗产地、国家AAAAA级旅游景区--龙虎山主景区排衙峰下,是一座独具现代园艺风格的花卉公园,园内汇集了3000余种花卉苗木,一年四季姹紫嫣红花香四溢.花园景观融合法、英、意、美、日、中六大经典园林风格,景观设计唯美新颖.玫瑰花园、香草花溪、台地花海、植物迷宫、儿童乐园等景点错落有致,交相呼应又自成一体,是世界园艺景观的大展示.该景区自2015年春建成试运行以来,每天游人如织,郁金香、向日葵、虞美人等赏花旺季日入园人数最高达万人.
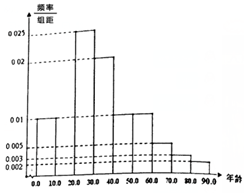
某学校社团为了解进园旅客的具体情形以及采集旅客对园区的建议,特别在2017年4月1日赏花旺季对进园游客进行取样调查,从当日12000名游客中抽取100人进行统计分析,结果如下:(表一)
(1)完成表格一中的空位①-④,并在答题卡中补全频率分布直方图,并估计2017年4月1日当日接待游客中30岁以下人数.
(2)完成表格二,并问你能否有97.5%的把握认为在观花游客中“年龄达到50岁以上”与“性别”相关?
(3)按分层抽样(分50岁以上与50以下两层)抽取被调查的100位游客中的10人作为幸运游客免费领取龙虎山内部景区门票,再从这10人中选取2人接受电视台采访,设这2人中年龄在50岁以上(含)的人数为ξ,求ξ的分布列
(表二)
(参考公式:k2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d)
 鹰潭市龙虎山花语世界位于中国第八处世界自然遗产,世界地质公元、国家自然文化双遗产地、国家AAAAA级旅游景区--龙虎山主景区排衙峰下,是一座独具现代园艺风格的花卉公园,园内汇集了3000余种花卉苗木,一年四季姹紫嫣红花香四溢.花园景观融合法、英、意、美、日、中六大经典园林风格,景观设计唯美新颖.玫瑰花园、香草花溪、台地花海、植物迷宫、儿童乐园等景点错落有致,交相呼应又自成一体,是世界园艺景观的大展示.该景区自2015年春建成试运行以来,每天游人如织,郁金香、向日葵、虞美人等赏花旺季日入园人数最高达万人.
鹰潭市龙虎山花语世界位于中国第八处世界自然遗产,世界地质公元、国家自然文化双遗产地、国家AAAAA级旅游景区--龙虎山主景区排衙峰下,是一座独具现代园艺风格的花卉公园,园内汇集了3000余种花卉苗木,一年四季姹紫嫣红花香四溢.花园景观融合法、英、意、美、日、中六大经典园林风格,景观设计唯美新颖.玫瑰花园、香草花溪、台地花海、植物迷宫、儿童乐园等景点错落有致,交相呼应又自成一体,是世界园艺景观的大展示.该景区自2015年春建成试运行以来,每天游人如织,郁金香、向日葵、虞美人等赏花旺季日入园人数最高达万人.某学校社团为了解进园旅客的具体情形以及采集旅客对园区的建议,特别在2017年4月1日赏花旺季对进园游客进行取样调查,从当日12000名游客中抽取100人进行统计分析,结果如下:(表一)
| 年龄 | 频数 | 频率 | 男 | 女 |
| [0,10) | 10 | 0.1 | 5 | 5 |
| [10,20) | ① | ② | ③ | ④ |
| [20,30) | 25 | 0.25 | 12 | 13 |
| [30,40) | 20 | 0.2 | 10 | 10 |
| [40,50) | 10 | 0.1 | 6 | 4 |
| [50,60) | 10 | 0.1 | 3 | 7 |
| [60,70) | 5 | 0.05 | 1 | 4 |
| [70,80) | 3 | 0.03 | 1 | 2 |
| [80,90) | 2 | 0.02 | 0 | 2 |
| 合计 | 100 | 1.00 | 45 | 55 |
(2)完成表格二,并问你能否有97.5%的把握认为在观花游客中“年龄达到50岁以上”与“性别”相关?
(3)按分层抽样(分50岁以上与50以下两层)抽取被调查的100位游客中的10人作为幸运游客免费领取龙虎山内部景区门票,再从这10人中选取2人接受电视台采访,设这2人中年龄在50岁以上(含)的人数为ξ,求ξ的分布列
(表二)
| 50岁以上 | 50岁以下 | 合计 | |
| 男生 | 5 | 40 | 45 |
| 女生 | 15 | 40 | 55 |
| 合计 | 20 | 80 | 100 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
20.已知集合A={x∈N|($\frac{1}{2}$)x≤1},B={x|x2-2x-8≤0},则A∩B=( )
| A. | {x|0≤x≤4} | B. | {0,1,2,3} | C. | {0,1,2,3,4} | D. | {1,2,3,4} |
1.已知函数f(x)=$\sqrt{3}$sin(2x+φ)+cos(2x+φ)为偶函数,且在[0,$\frac{π}{4}$]上是增函数,则φ的一个可能值为( )
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{4π}{3}$ | D. | $\frac{5π}{3}$ |