题目内容
12.《九章算术》卷第六《均输》中,有问题“今有竹九节,下三节容量四升,上四节容量三升.问中间二节欲均容,各多少?”其中“欲均容”的意思是:使容量变化均匀,即由下往上均匀变细.在这个问题中的中间两节容量和是( )| A. | $1\frac{61}{66}$升 | B. | 2升 | C. | $2\frac{3}{22}$升 | D. | 3升 |
分析 利用已知条件列出方程组,利用等差数列求出首项与公差,然后求解即可.
解答 解:设竹九节由上往下的容量分别为a1,a2,a3,a4,a5,a6,a7,a8,a9,
由题意可知:$\left\{\begin{array}{l}{a_1}+{a_2}+{a_3}+{a_4}=3\\{a_7}+{a_8}+{a_9}=4\end{array}\right.$$⇒\left\{\begin{array}{l}{a_1}=\frac{13}{22}\\ d=\frac{7}{66}\end{array}\right.$,
所以问题中的中间两节容量和为a5+a6=2a1+9d=$\frac{47}{22}$
=$2\frac{3}{22}$.
故选:C.
点评 本题考查等差数列的应用,判断数列是等差数列是解题的关键,考查计算能力.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
2.网络购物已经成为一种时尚,电商们为了提升知名度,加大了在媒体上的广告投入.经统计,近五年某电商在媒体上的广告投入费用x(亿元)与当年度该电商的销售收入y(亿元)的数据如下表:):
(Ⅰ)求y关于x的回归方程;
(Ⅱ)2017年度该电商准备投入广告费1.5亿元,利用(Ⅰ)中的回归方程,预测该电商2017年的销售收入.
附:回归直线的斜率和截距的最小二乘估计公式分别为:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n•\overline{x}•\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n•{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$•$\overline{x}$,选用数据:$\sum_{i=1}^{5}$xiyi=123.1,$\sum_{i=1}^{5}$x${\;}_{i}^{2}$=5.1.
| 年份 | 2012年 | 2013年 | 2014 | 2015 | 2016 |
| 广告投入x | 0.8 | 0.9 | 1 | 1.1 | 1.2 |
| 销售收入y | 16 | 23 | 25 | 26 | 30 |
(Ⅱ)2017年度该电商准备投入广告费1.5亿元,利用(Ⅰ)中的回归方程,预测该电商2017年的销售收入.
附:回归直线的斜率和截距的最小二乘估计公式分别为:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n•\overline{x}•\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n•{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$•$\overline{x}$,选用数据:$\sum_{i=1}^{5}$xiyi=123.1,$\sum_{i=1}^{5}$x${\;}_{i}^{2}$=5.1.
3.已知函数f(x)在R上可导,则“f'(x0)=0”是“f(x0)为函数f(x)的极值”的( )
| A. | 充分不必要条件 | B. | 充要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
17.若$\frac{1}{a}$<$\frac{1}{b}$<0,则下列结论正确的是( )
| A. | a2>b2 | B. | 1>($\frac{1}{2}$)b>($\frac{1}{2}$)a | C. | $\frac{b}{a}$+$\frac{a}{b}$<2 | D. | aeb>bea |
1.已知复数z满足z•(2+i)=i,i为虚数单位,则|$\overline{z}$|的值为( )
| A. | $\frac{\sqrt{5}}{5}$ | B. | $\sqrt{5}$ | C. | 1 | D. | $\frac{2\sqrt{5}}{5}$ |
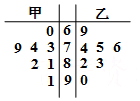 某人到甲、乙两市各7个小区调查空置房情况,调查得到的小区空置房的套数绘成了如图的茎叶图,则调查中甲市空置房套数的中位数与乙市空置房套数的中位数之差为( )
某人到甲、乙两市各7个小区调查空置房情况,调查得到的小区空置房的套数绘成了如图的茎叶图,则调查中甲市空置房套数的中位数与乙市空置房套数的中位数之差为( )