18．
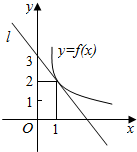如图所示，y=f（x）是可导函数，直线l：y=kx+3是曲线y=f（x）在x=1处的切线，令h（x）=xf（x），h′（x）是h（x）的导函数，则h′（1）的值是（ ）
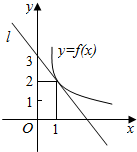如图所示，y=f（x）是可导函数，直线l：y=kx+3是曲线y=f（x）在x=1处的切线，令h（x）=xf（x），h′（x）是h（x）的导函数，则h′（1）的值是（ ）| A． | 2 | B． | 1 | C． | -1 | D． | $\frac{1}{2}$ |
11．已知奇函数f（x）满足f（x+2）=-f（x），且当x∈（0，1）时，f（x）=2x，则$f（\frac{7}{2}）$的值为（ ）
| A． | $-\sqrt{2}$ | B． | $\frac{1}{2}$ | C． | $\sqrt{2}$ | D． | 4 |
10．已知角θ满足sinθ-2cosθ=0，则$\frac{{cos（\frac{3π}{2}+θ）+4cos（π-θ）}}{{sin（\frac{π}{2}-θ）-sin（π-θ）}}$=（ ）
| A． | -2 | B． | 0 | C． | $\frac{2}{3}$ | D． | 2 |
9．已知函数$f（x）=\left\{\begin{array}{l}x，|x|≤1\\ sin\frac{π}{2}x，|x|＞1\end{array}\right.$则下列结论正确的是（ ）
0 225103 225111 225117 225121 225127 225129 225133 225139 225141 225147 225153 225157 225159 225163 225169 225171 225177 225181 225183 225187 225189 225193 225195 225197 225198 225199 225201 225202 225203 225205 225207 225211 225213 225217 225219 225223 225229 225231 225237 225241 225243 225247 225253 225259 225261 225267 225271 225273 225279 225283 225289 225297 266669
| A． | ?x0∈R，f（-x0）≠-f（x0） | B． | ?x∈R，f（-x）≠f（x） | ||
| C． | 函数f（x）在$[-\frac{π}{2}，\frac{π}{2}]$上单调递增 | D． | 函数f（x）的值域是[-1，1] |