题目内容
17.如图,在矩形ABCD中,已知AB=3,AD=2,且$\overrightarrow{BE}$=$\overrightarrow{EC}$,$\overrightarrow{DF}$=$\frac{1}{2}\overrightarrow{FC}$,则$\overrightarrow{AE}$•$\overrightarrow{BF}$=-4.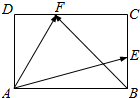
分析 建立平面直角坐标系,求出$\overrightarrow{AE},\overrightarrow{BF}$的坐标,代入数量积公式计算.
解答  解:以AB为x轴,以AD为y轴建立平面直角坐标系,则A(0,0),B(3,0),E(3,1),F(1,2).
解:以AB为x轴,以AD为y轴建立平面直角坐标系,则A(0,0),B(3,0),E(3,1),F(1,2).
∴$\overrightarrow{AE}$=(3,1),$\overrightarrow{BF}$=(-2,2).∴$\overrightarrow{AE}$•$\overrightarrow{BF}$=-6+2=-4.
故答案为-4.
点评 本题考查了平面向量的数量积运算,建立坐标系可简化数量积运算,是基础题.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
8.设x,y满足约束条件$\left\{\begin{array}{l}{x+y≥3}\\{x-y≥-1}\\{2x-y≤3}\end{array}\right.$,则目标函数z=x+y的最大值为9.
5.抛物线x2=4y的准线与y轴的交点的坐标为( )
| A. | $(0,-\frac{1}{2})$ | B. | (0,-1) | C. | (0,-2) | D. | (0,-4) |
6.点P在边长为1的正方形ABCD内运动,则动点P到顶点A的距离|PA|≤1概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{π}{4}$ | D. | π |
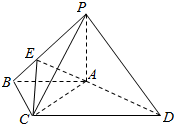 如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB∥CD,∠ABC=∠CAD=90°,点E在棱PB上,且PE=2EB,PA=AB=BC.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB∥CD,∠ABC=∠CAD=90°,点E在棱PB上,且PE=2EB,PA=AB=BC.