题目内容
13.函数f(x)=ax3-sinbx+2015(x∈R),若$f(\frac{π}{4})=1$,则$f(-\frac{π}{4})$=4029.分析 利用函数的奇偶性以及函数值求解即可.
解答 解:函数f(x)=ax3-sinbx+2015(x∈R),若$f(\frac{π}{4})=1$,
可得a($\frac{π}{4}$)3-sinb$\frac{π}{4}$+2015=1,
可得a($\frac{π}{4}$)3-sinb$\frac{π}{4}$=-2014.
$f(-\frac{π}{4})$=-[a($\frac{π}{4}$)3-sinb$\frac{π}{4}$]+2015=2014+2015=4029.
故答案为:4029.
点评 本题考查函数的奇偶性的应用,函数值的求法,考查计算能力.

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
1.函数f(x)=log0.5(x-1)的定义域为( )
| A. | (-1,+∞) | B. | (1,+∞) | C. | (0,+∞) | D. | (-∞,0) |
18.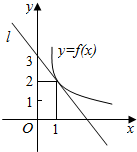 如图所示,y=f(x)是可导函数,直线l:y=kx+3是曲线y=f(x)在x=1处的切线,令h(x)=xf(x),h′(x)是h(x)的导函数,则h′(1)的值是( )
如图所示,y=f(x)是可导函数,直线l:y=kx+3是曲线y=f(x)在x=1处的切线,令h(x)=xf(x),h′(x)是h(x)的导函数,则h′(1)的值是( )
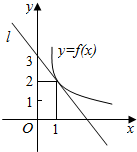 如图所示,y=f(x)是可导函数,直线l:y=kx+3是曲线y=f(x)在x=1处的切线,令h(x)=xf(x),h′(x)是h(x)的导函数,则h′(1)的值是( )
如图所示,y=f(x)是可导函数,直线l:y=kx+3是曲线y=f(x)在x=1处的切线,令h(x)=xf(x),h′(x)是h(x)的导函数,则h′(1)的值是( )| A. | 2 | B. | 1 | C. | -1 | D. | $\frac{1}{2}$ |
5.下列函数中,是奇函数,又是定义域内为减函数的是( )
| A. | y=|$\frac{1}{2}$|x | B. | y=$\frac{1}{x}$ | C. | y=-x3 | D. | y=x2 |