题目内容
14.已知函数f(x)=-2x2+mx-3为区间(-5,-3+n)内的偶函数.(1)求实数m,n的值;
(2)求函数f(x)在区间[1,5]上的最小值.
分析 (1)利用二次函数是偶函数,求出m,区间对称求出n即可.
(2)利用二次函数的对称性以及开口方向求解函数的最值.
解答 解:(1)因为函数f(x)=-2x2+mx-3为区间(-5,-3+n)内的偶函数
所以m=0…(3分)
且-3+n=5,得n=8…(5分)
(2)由(1)知f(x)=-2x2-3
则函数f(x)在[0,+∞)上单调递减…(7分)
在(-∞,0]上单调递增…(9分)
故函数f(x)在[1,5]上单调递减…(10分)
所以函数f(x)在区间[1,5]上的最小值为f(x)min=f(5)=-53…(12分)
点评 本题考查二次函数的简单性质的应用,考查计算能力.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
14.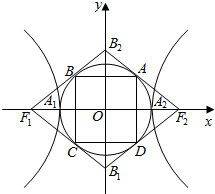 我们把离心率为$\frac{\sqrt{5}+1}{2}$的双曲线叫做黄金双曲线.如图,黄金双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)的两顶点为A1,A2,虚轴两端点为B1,B2,两焦点为F1,F2,若以A1,A2为直径的圆内切于菱形F1B1F2B2,切点分别为A,B,C,D,则菱形F1B1F2B2的面积S1与矩形ABCD的面积S2的比值$\frac{{S}_{1}}{{S}_{2}}$=( )
我们把离心率为$\frac{\sqrt{5}+1}{2}$的双曲线叫做黄金双曲线.如图,黄金双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)的两顶点为A1,A2,虚轴两端点为B1,B2,两焦点为F1,F2,若以A1,A2为直径的圆内切于菱形F1B1F2B2,切点分别为A,B,C,D,则菱形F1B1F2B2的面积S1与矩形ABCD的面积S2的比值$\frac{{S}_{1}}{{S}_{2}}$=( )
 我们把离心率为$\frac{\sqrt{5}+1}{2}$的双曲线叫做黄金双曲线.如图,黄金双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)的两顶点为A1,A2,虚轴两端点为B1,B2,两焦点为F1,F2,若以A1,A2为直径的圆内切于菱形F1B1F2B2,切点分别为A,B,C,D,则菱形F1B1F2B2的面积S1与矩形ABCD的面积S2的比值$\frac{{S}_{1}}{{S}_{2}}$=( )
我们把离心率为$\frac{\sqrt{5}+1}{2}$的双曲线叫做黄金双曲线.如图,黄金双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)的两顶点为A1,A2,虚轴两端点为B1,B2,两焦点为F1,F2,若以A1,A2为直径的圆内切于菱形F1B1F2B2,切点分别为A,B,C,D,则菱形F1B1F2B2的面积S1与矩形ABCD的面积S2的比值$\frac{{S}_{1}}{{S}_{2}}$=( )| A. | $\frac{\sqrt{5}+2}{2}$ | B. | $\frac{\sqrt{5}+1}{2}$ | C. | $\frac{\sqrt{5}-2}{2}$ | D. | $\frac{\sqrt{5}-1}{2}$ |
9.已知函数$f(x)=\left\{\begin{array}{l}x,|x|≤1\\ sin\frac{π}{2}x,|x|>1\end{array}\right.$则下列结论正确的是( )
| A. | ?x0∈R,f(-x0)≠-f(x0) | B. | ?x∈R,f(-x)≠f(x) | ||
| C. | 函数f(x)在$[-\frac{π}{2},\frac{π}{2}]$上单调递增 | D. | 函数f(x)的值域是[-1,1] |
4.某市交警部门为了解本市实习期司机对新交通法规的掌握情况,随机对100名实习期司机进行调查,调查问卷共10道题,答题情况如下表:
(Ⅰ)如果实习期司机答对题目数不少于9道,就认为该实习期司机对新交通法规的掌握情况比较好,试估计该市实习期司机对新交通法规掌握情况比较好的概率;
(Ⅱ)从答对题目数不少于8道的实习期司机中任意选出两人做进一步的调查,求选出的两人中至少有一名女实习期司机的概率.
| 答对题目数 | 小于8 | 8 | 9 | 10 |
| 女 | 2 | 13 | 12 | 8 |
| 男 | 3 | 37 | 16 | 9 |
(Ⅱ)从答对题目数不少于8道的实习期司机中任意选出两人做进一步的调查,求选出的两人中至少有一名女实习期司机的概率.
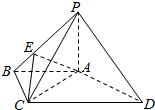 如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB∥CD,∠ABC=90°,且CD=2AB,点E在棱PB上,且PE=2EB,PA=AB=BC.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB∥CD,∠ABC=90°,且CD=2AB,点E在棱PB上,且PE=2EB,PA=AB=BC.