题目内容
10.已知角θ满足sinθ-2cosθ=0,则$\frac{{cos(\frac{3π}{2}+θ)+4cos(π-θ)}}{{sin(\frac{π}{2}-θ)-sin(π-θ)}}$=( )| A. | -2 | B. | 0 | C. | $\frac{2}{3}$ | D. | 2 |
分析 利用诱导公式化简所求的表达式,代入已知条件求解即可.
解答 解:角θ满足sinθ-2cosθ=0,
则$\frac{{cos(\frac{3π}{2}+θ)+4cos(π-θ)}}{{sin(\frac{π}{2}-θ)-sin(π-θ)}}$=$\frac{sinθ-4cosθ}{cosθ-sinθ}$=$\frac{2cosθ-4cosθ}{cosθ-2cosθ}$=2.
故选:D.
点评 本题考查诱导公式的应用,三角函数的化简求值,考查计算能力.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目
1.某中药种植基地有两处种植区的药材需在下周一、周二两天内采摘完毕,基地员工一天可以完成一处种植区的采摘,由于下雨会影响药材品质,基地收益如下表所示:
若基地额外聘请工人,可在周一当天完成全部采摘任务;无雨时收益为20万元;有雨时收益为10万元,额外聘请工人的成本为a万元.已知下周一和下周二有雨的概率相同,两天是否下雨互不影响,基地收益为20万元的概率为0.36.(1)若不额外聘请工人,写出基地收益X的分布列及基地的预期收益;
(2)该基地是否应该外聘工人,请说明理由.
| 周一 | 无雨 | 无雨 | 有雨 | 有雨 |
| 周二 | 无雨 | 有雨 | 无雨 | 有雨 |
| 收益 | 20万 | 15万 | 10万 | 7.5万 |
(2)该基地是否应该外聘工人,请说明理由.
5.抛物线x2=4y的准线与y轴的交点的坐标为( )
| A. | $(0,-\frac{1}{2})$ | B. | (0,-1) | C. | (0,-2) | D. | (0,-4) |
19.已知函数f(x)=kx-1,其中实数k随机选自区间[-1,2].则对任意的x∈[-1,1],f(x)≤0的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
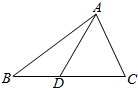 如图,在△ABC中,AB=12,$AC=3\sqrt{6}$,$BC=5\sqrt{6}$,点D在边BC上,且∠ADC=60°.
如图,在△ABC中,AB=12,$AC=3\sqrt{6}$,$BC=5\sqrt{6}$,点D在边BC上,且∠ADC=60°.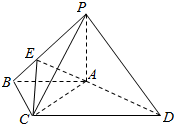 如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB∥CD,∠ABC=∠CAD=90°,点E在棱PB上,且PE=2EB,PA=AB=BC.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB∥CD,∠ABC=∠CAD=90°,点E在棱PB上,且PE=2EB,PA=AB=BC.