题目内容
18．
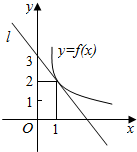如图所示，y=f（x）是可导函数，直线l：y=kx+3是曲线y=f（x）在x=1处的切线，令h（x）=xf（x），h′（x）是h（x）的导函数，则h′（1）的值是（ ）| A． | 2 | B． | 1 | C． | -1 | D． | $\frac{1}{2}$ |
分析 根据导数的几何意义求出切线斜率，利用导数的运算法则进行求解即可得到结论．
解答 解：由图象可知直线的切线经过点（1，2），则k+3=2，得k=-1，
即f′（1）=-1，且f（1）=2，
∵h（x）=xf（x），
∴h′（x）=f（x）+xf′（x），
则h′（1）=f（1）+f′（1）=2-1=1，
故选：B．
点评 本题主要考查导数的计算利用导数的几何意义和导数的运算法则是解决本题的关键．
练习册系列答案
浙江名校名师金卷系列答案
相关题目
18．一元二次方程x2-2ix-5=0的根的情况是（ ）
| A． | 有两个不等的实根 | B． | 有一个实根和一个虚根 | ||
| C． | 有一对共轭的虚根 | D． | 有两个不共轭的虚根 |
6．某程序框图如图所示，执行该程序，若输入的a值为1，则输出的a值为（ ）
| A． | 1 | B． | 2 | C． | 3 | D． | 5 |
10．若两条直线ax+2y+6=0与x+（a-1）y+（a2-1）=0平行，则a的取值集合是（ ）
| A． | {-1，2} | B． | {-1} | C． | {2} | D． | $\left\{{\frac{2}{3}}\right\}$ |