2.一个三棱锥的三视图如图所示,则它的体积为( )
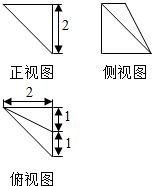

| A. | $\frac{2}{3}$ | B. | 1 | C. | $\frac{4}{3}$ | D. | 2 |
1.若抛物线C1:y=$\frac{1}{4}$x2的焦点F到双曲线C2:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一条渐近线的距离为$\frac{\sqrt{3}}{2}$,抛物线C1上的动点P到双曲线C2的一个焦点的距离与到直线y=-1的距离之和的最小时为$\sqrt{5}$,则双曲线C2的方程为( )
| A. | $\frac{{x}^{2}}{3}$-y2=1 | B. | x2-$\frac{{y}^{2}}{3}$=1 | C. | $\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{2}$=1 | D. | $\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{3}$=1 |
20.已知△ABC的边BC上一动点D满足$\overrightarrow{CD}$=n$\overrightarrow{DB}$(n∈N*),$\overrightarrow{AD}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$,则数列{(n+1)x}的前n项和为( )
| A. | $\frac{1}{n+1}$ | B. | $\frac{n}{n+1}$ | C. | $\frac{1}{2}n(n+1)$ | D. | $\frac{1}{2}(n+1)(n+2)$ |
19.在△ABC中,角A,B,C所对的边分别为a,b,c,若a=$\sqrt{3}$,且a2=b2+c2-bc,则△ABC的面积S的最大值为( )
| A. | $\frac{\sqrt{3}}{4}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{3\sqrt{3}}{4}$ | D. | $\sqrt{3}$ |
18.已知实数x,y满足$\left\{\begin{array}{l}{2x+y-2≥0}\\{kx-y+2≥0}\\{y≥0}\end{array}\right.$,且目标函数z=y-x取得最小值-4,则k等于( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | -$\frac{1}{4}$ | D. | -$\frac{1}{2}$ |
17.某中学高一、高二各有一个文科和一个理科两个实验班,现将这四个班级随机分配到上海交通大学和浙江大学两所高校进行研学,每个班级去一所高校,每所高校至少有一个班级去,则恰好有一个文科班和一个理科班分配到上海交通大学的概率为( )
| A. | $\frac{1}{7}$ | B. | $\frac{2}{7}$ | C. | $\frac{3}{7}$ | D. | $\frac{4}{7}$ |
16.将函数y=cos2x的图象向右平移φ个单位得到函数y=cos2x-$\sqrt{3}$sin2x的图象,则φ的一个可能取值为( )
0 224601 224609 224615 224619 224625 224627 224631 224637 224639 224645 224651 224655 224657 224661 224667 224669 224675 224679 224681 224685 224687 224691 224693 224695 224696 224697 224699 224700 224701 224703 224705 224709 224711 224715 224717 224721 224727 224729 224735 224739 224741 224745 224751 224757 224759 224765 224769 224771 224777 224781 224787 224795 266669
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |