题目内容
20.已知△ABC的边BC上一动点D满足$\overrightarrow{CD}$=n$\overrightarrow{DB}$(n∈N*),$\overrightarrow{AD}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$,则数列{(n+1)x}的前n项和为( )| A. | $\frac{1}{n+1}$ | B. | $\frac{n}{n+1}$ | C. | $\frac{1}{2}n(n+1)$ | D. | $\frac{1}{2}(n+1)(n+2)$ |
分析 通过$\overrightarrow{CD}$=n$\overrightarrow{DB}$(n∈N*)可知$\overrightarrow{AD}$=$\frac{n}{n+1}$$\overrightarrow{AB}$+$\frac{1}{n+1}$$\overrightarrow{AC}$,与$\overrightarrow{AD}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$比较可得x=$\frac{n}{n+1}$,进而计算可得结论.
解答 解:∵$\overrightarrow{CD}$=n$\overrightarrow{DB}$(n∈N*),
∴$\overrightarrow{AD}$=$\frac{n}{n+1}$$\overrightarrow{AB}$+$\frac{1}{n+1}$$\overrightarrow{AC}$,
又∵$\overrightarrow{AD}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$,
∴x=$\frac{n}{n+1}$,
∴数列{(n+1)x}是首项、公差均为1的等差数列,
∴则数列{(n+1)x}的前n项和为$\frac{n(n+1)}{2}$,
故选:C.
点评 本题考查数列的通项及前n项和,考查运算求解能力,注意解题方法的积累,属于中档题.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
10.函数$f(x)=\frac{{\sqrt{x+2}}}{x-1}$的定义域为( )
| A. | {x|x≥-2且x≠1} | B. | {x|x≥-2} | C. | {x|x≥-2或x≠1} | D. | {x|x≠1} |
8.“x>y>0,m<n<0“是“xm<ny”的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既非充分又非必要条件 |
15.截至11月27日,国内某球员在2015-2016赛季CBA联赛的前10轮比赛中,各场得分xi(i=1,2,3,…,10)的茎叶图如图①所示,图②是该运动员某项成绩指标分析的程序框图,则输出的结果是( )


| A. | 8 | B. | 7 | C. | 6 | D. | 5 |
10.若函数$f(x)=2sin(ωx+\frac{π}{3}),x∈R$,又f(m)=-2,f(n)=0,且|m-n|的最小值为$\frac{3π}{4}$,则正数ω的值是( )
| A. | $\frac{2}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{3}{2}$ |
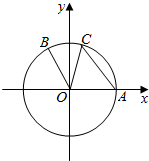 如图,在平面直角坐标系xOy中,以原点为圆心的圆O与x轴的正半轴交于点A,点B(-1,2)在圆O上,点C在弧AB上,且∠BOC为$\frac{π}{4}$.
如图,在平面直角坐标系xOy中,以原点为圆心的圆O与x轴的正半轴交于点A,点B(-1,2)在圆O上,点C在弧AB上,且∠BOC为$\frac{π}{4}$.