题目内容
4.已知正数x,y满足2x+y=1,则4x2+y2+$\frac{1}{xy}$的最小值为$\frac{17}{2}$.分析 由基本不等式可得0<xy≤$\frac{1}{8}$,令t=xy,0<t≤$\frac{1}{8}$,由4t-$\frac{1}{t}$在0<t≤$\frac{1}{8}$递增,可得最小值.
解答 解:正数x,y满足2x+y=1,
可得2x+y≥2$\sqrt{2xy}$,
即有0<xy≤$\frac{1}{8}$,
则4x2+y2+$\frac{1}{xy}$=(2x+y)2-4xy+$\frac{1}{xy}$
=1-(4xy-$\frac{1}{xy}$),
令t=xy,0<t≤$\frac{1}{8}$,
由4t-$\frac{1}{t}$在0<t≤$\frac{1}{8}$递增,
可得t=$\frac{1}{8}$时,4t-$\frac{1}{t}$取得最大值,且为-$\frac{15}{2}$,
则4x2+y2+$\frac{1}{xy}$在xy=$\frac{1}{8}$时,取得最小值,且为1+$\frac{15}{2}$=$\frac{17}{2}$.
故答案为:$\frac{17}{2}$.
点评 本题考查基本不等式的运用:求最值,同时考查配方法和函数的单调性的运用,考查运算能力,属于中档题.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
14.已知${2^x}>{(\frac{1}{2})^{x-1}}$,则x的取值范围是( )
| A. | R | B. | $x<\frac{1}{2}$ | C. | $x>\frac{1}{2}$ | D. | ∅ |
15.某校现有高一学生210人,高二学生270人,高三学生240人,用分层抽样的方法从这三个年级的学生中随机抽取n名学生进行问卷调查,如果已知从高一学生中抽取的人数为7,那么从高三学生中抽取的人数应为( )
| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
19.在△ABC中,角A,B,C所对的边分别为a,b,c,若a=$\sqrt{3}$,且a2=b2+c2-bc,则△ABC的面积S的最大值为( )
| A. | $\frac{\sqrt{3}}{4}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{3\sqrt{3}}{4}$ | D. | $\sqrt{3}$ |
16.函数f(x)=sin(x+$\frac{π}{4}$)图象的一条对称轴方程为( )
| A. | x=-$\frac{π}{4}$ | B. | x=$\frac{π}{4}$ | C. | x=$\frac{π}{2}$ | D. | x=π |
13.某变速运动的物体,路程s(米)随时间t(秒)变化的函数关系式是s=t2-2t+5,则此物体在t=1秒时的瞬时速度为( )
| A. | 2m/s | B. | 0m/s | C. | 4m/s | D. | -4m/s |
14.函数f(x)=$\frac{1}{x^2}$+1的图象关于( )
| A. | y轴对称 | B. | 直线y=-x对称 | C. | 坐标原点对称 | D. | 直线y=x对称 |
 设函数f(x)=log2(x-a)(a∈R).
设函数f(x)=log2(x-a)(a∈R).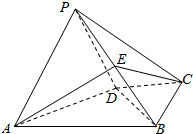 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB∥CD,∠ABC=90°,AB=2,AD=$\sqrt{2}$,PA=PD=CD=CB=1,E总是线段PB上的动点.
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB∥CD,∠ABC=90°,AB=2,AD=$\sqrt{2}$,PA=PD=CD=CB=1,E总是线段PB上的动点.