题目内容
16.将函数y=cos2x的图象向右平移φ个单位得到函数y=cos2x-$\sqrt{3}$sin2x的图象,则φ的一个可能取值为( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
分析 由和差角的公式化简可得y=2cos2(x-$\frac{5π}{6}$),由三角函数图象变换的规则可得.
解答 解:∵y=cos2x-$\sqrt{3}$sin2x=2cos(2x+$\frac{π}{3}$)=2cos(2x-$\frac{5π}{3}$)=2cos2(x-$\frac{5π}{6}$),
∴φ的一个可能取值为$\frac{5π}{6}$.
故选:D.
点评 本题考查两角和与差的三角函数公式,涉及三角函数图象的变换,属基础题.

练习册系列答案
相关题目
1.若抛物线C1:y=$\frac{1}{4}$x2的焦点F到双曲线C2:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一条渐近线的距离为$\frac{\sqrt{3}}{2}$,抛物线C1上的动点P到双曲线C2的一个焦点的距离与到直线y=-1的距离之和的最小时为$\sqrt{5}$,则双曲线C2的方程为( )
| A. | $\frac{{x}^{2}}{3}$-y2=1 | B. | x2-$\frac{{y}^{2}}{3}$=1 | C. | $\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{2}$=1 | D. | $\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{3}$=1 |
5.信息时代,学生广泛使用手机,从某校学生中随机抽取200名,这200名学生中上课时间和不上时间都不使用手机的共有37人,这200名学生每天在校使用手机情况如下表:
利用以上数据,将统计的频率视为概率.
(1)求上表中m、n的值;
(2)求该校学生上课时间使用手机的概率.
| 分类 人数(人) 时间 | 一小时以上 | 一小时以内 | 不使用 | 合计 |
| 上课时间 | 23 | 55 | m | 98 |
| 不上课时间 | 17 | 68 | 17 | 102 |
| 合计 | 40 | 123 | n | 200 |
(1)求上表中m、n的值;
(2)求该校学生上课时间使用手机的概率.
 如图,在长方体OADB-CA1D1B1中,OA=3,OB=4,OC=2,OI=OJ=OK=1,点E,F分别是DB,D1B1的中点.设$\overrightarrow{OI}$=$\overrightarrow{i}$,$\overrightarrow{OJ}$=$\overrightarrow{j}$,$\overrightarrow{OK}$=$\overrightarrow{k}$,试用向量$\overrightarrow{i}$,$\overrightarrow{j}$,$\overrightarrow{k}$表示$\overrightarrow{O{D}_{1}}$、$\overrightarrow{O{A}_{1}}$、$\overrightarrow{OE}$、$\overrightarrow{OF}$.
如图,在长方体OADB-CA1D1B1中,OA=3,OB=4,OC=2,OI=OJ=OK=1,点E,F分别是DB,D1B1的中点.设$\overrightarrow{OI}$=$\overrightarrow{i}$,$\overrightarrow{OJ}$=$\overrightarrow{j}$,$\overrightarrow{OK}$=$\overrightarrow{k}$,试用向量$\overrightarrow{i}$,$\overrightarrow{j}$,$\overrightarrow{k}$表示$\overrightarrow{O{D}_{1}}$、$\overrightarrow{O{A}_{1}}$、$\overrightarrow{OE}$、$\overrightarrow{OF}$.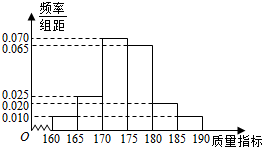 从某企业的一种产品中抽取40件产品,测量其某项质量指标,测量结果的频率分布直方图如图所示.
从某企业的一种产品中抽取40件产品,测量其某项质量指标,测量结果的频率分布直方图如图所示.