题目内容
3.函数f(x)=1+x-$\frac{{x}^{2}}{2}$+$\frac{{x}^{3}}{3}$-$\frac{{x}^{4}}{4}$+…+$\frac{{x}^{2015}}{2015}$-$\frac{{x}^{2016}}{2016}$在区间[-2,2]上的零点个数为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 求导f′(x)=1-x+x2-x3+…+x2014-x2015,分类讨论以确定f(x)的单调性,从而确定函数的极值的正负,从而利用函数的零点判定定理判断即可.
解答 解:∵f(x)=1+x-$\frac{{x}^{2}}{2}$+$\frac{{x}^{3}}{3}$-$\frac{{x}^{4}}{4}$+…+$\frac{{x}^{2015}}{2015}$-$\frac{{x}^{2016}}{2016}$,
∴f′(x)=1-x+x2-x3+…+x2014-x2015,
当x=-1时,f′(x)=2016>0,
当x≠-1时,f′(x)=$\frac{1-{x}^{2016}}{1+x}$,
故当-2<x<-1或-1<x<1时,f′(x)>0;
当1<x<2时,f′(x)<0;
故f(x)在[-2,1]上单调递增,在(1,2]上单调递减,
又∵f(-2)<0,f(1)>0,f(2)<0,
∴f(x)在(-2,1)和(1,2)内各有一个零点,
故选:B.
点评 本题考查了导数的综合应用及分类讨论的思想应用,同时考查了零点的判定定理的应用.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
13.下列函数中,在(0,+∞)上为增函数的是( )
| A. | y=-x2 | B. | $y={(\frac{1}{π})^x}$ | C. | $y={log_{\frac{1}{2}}}x$ | D. | $y=\sqrt{x}$ |
18.已知实数x,y满足$\left\{\begin{array}{l}{2x+y-2≥0}\\{kx-y+2≥0}\\{y≥0}\end{array}\right.$,且目标函数z=y-x取得最小值-4,则k等于( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | -$\frac{1}{4}$ | D. | -$\frac{1}{2}$ |
15.设集合A={x|x2-x≤0},B={0,1,2},则A∩B=( )
| A. | ∅ | B. | {0} | C. | {0,1} | D. | {0,1,2} |
12.在等差数列{an}中,a2=0,a4=4,则{an}的前5项和S5=( )
| A. | 20 | B. | 14 | C. | 12 | D. | 10 |
13.已知函数f(x)=$\frac{1}{{\sqrt{3-x}}}$的定义域为M,g(x)=$\sqrt{x+1}$的定义域为N,则M∩N=( )
| A. | {x|x≥-1} | B. | {x|x<3} | C. | {x|-1<x<3} | D. | {x|-1≤x<3} |
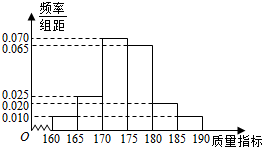 从某企业的一种产品中抽取40件产品,测量其某项质量指标,测量结果的频率分布直方图如图所示.
从某企业的一种产品中抽取40件产品,测量其某项质量指标,测量结果的频率分布直方图如图所示.