题目内容
5.若对于任意实数t,圆C1:(x+4)2+y2=1与圆C2:(x-t)2+(y-at+2)2=1都没有公共点,则实数a的取值范围是a<-$\frac{4}{3}$或a>0.分析 通过两个圆的方程求出两个圆的圆心与半径,利用圆心距与半径和与差的关系即可求解.
解答 解:圆C2:(x-t)2+(y-at+2)2=1的圆心在直线y=ax-2上,
∴要使圆C1:(x+4)2+y2=1与圆C2:(x-t)2+(y-at+2)2=1没有公共点,
必须使圆心C1(-4,0)到直线y=ax-2的距离大于两圆半径之和,即d=$\frac{|-4a-2|}{\sqrt{{a}^{2}+1}}$>2,
∴a<-$\frac{4}{3}$或a>0.
故答案为:a<-$\frac{4}{3}$或a>0.
点评 本题考查两个圆的位置关系的应用,考查转化思想,计算能力,属于中档题.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
15.下列幂函数在(-∞,0)上为减函数的是( )
| A. | y=x${\;}^{\frac{1}{3}}$ | B. | y=x3 | C. | y=x2 | D. | y=x |
16.甲、乙两人各自独立随机地从区间[0,1]任取一数,分别记为x、y,则x2+y2>1的概率P=( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{π}{4}$ | D. | 1$-\frac{π}{4}$ |
13.已知集合A={y|y=x${\;}^{\frac{1}{2}}$},B={y|y=($\frac{1}{2}$)x,x>1},则A∩B=( )
| A. | (0,$\frac{1}{2}$) | B. | ($\frac{1}{2},1$) | C. | (0,1) | D. | ∅ |
20.已知△ABC的边BC上一动点D满足$\overrightarrow{CD}$=n$\overrightarrow{DB}$(n∈N*),$\overrightarrow{AD}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$,则数列{(n+1)x}的前n项和为( )
| A. | $\frac{1}{n+1}$ | B. | $\frac{n}{n+1}$ | C. | $\frac{1}{2}n(n+1)$ | D. | $\frac{1}{2}(n+1)(n+2)$ |
10.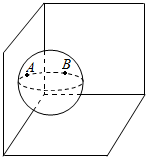 一个球由于某种原因其直径无法直接测量,有人设计了这么一个测量方法:把球外面涂上颜料滚到一个房子的屋角使得球与两堵墙相切,沾到颜料的地方A,B就是切点(如图),若量得|AB|=28.3cm,则此球的直径约为( )
一个球由于某种原因其直径无法直接测量,有人设计了这么一个测量方法:把球外面涂上颜料滚到一个房子的屋角使得球与两堵墙相切,沾到颜料的地方A,B就是切点(如图),若量得|AB|=28.3cm,则此球的直径约为( )
 一个球由于某种原因其直径无法直接测量,有人设计了这么一个测量方法:把球外面涂上颜料滚到一个房子的屋角使得球与两堵墙相切,沾到颜料的地方A,B就是切点(如图),若量得|AB|=28.3cm,则此球的直径约为( )
一个球由于某种原因其直径无法直接测量,有人设计了这么一个测量方法:把球外面涂上颜料滚到一个房子的屋角使得球与两堵墙相切,沾到颜料的地方A,B就是切点(如图),若量得|AB|=28.3cm,则此球的直径约为( )| A. | 20cm | B. | 40cm | C. | 28.3cm | D. | 34.6cm |
17.某程序框图如图所示,若运行该程序后输出S=( )


| A. | $\frac{5}{3}$ | B. | $\frac{7}{4}$ | C. | $\frac{9}{5}$ | D. | $\frac{11}{6}$ |
14.在△ABC中,角A,B,C所对的边分别是a,b,c且a=3,b=$\sqrt{3}$,面积为$\frac{3\sqrt{3}}{4}$,则边c的长为( )
| A. | $\sqrt{3}$ | B. | $\sqrt{21}$ | C. | $\sqrt{3}$或$\sqrt{21}$ | D. | $\sqrt{6}$ |
15.已知f(x-1)=x2+1,则f(x)的表达式为( )
| A. | f(x)=x2+1 | B. | f(x)=(x+1)2+1 | C. | f(x)=(x-1)2+1 | D. | f(x)=x2 |