设z=1-i(i是虚数单位),则复数
的虚部是( )
| 2 |
| z |
| A、1 | B、-1 | C、i | D、-i |
现有10个数,它们能构成一个以1为首项,-3为公比的等比数列,若从这10个数中随机抽取一个数,则它小于8的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
设F1,F2为椭圆C1:
+
=1(a>b>0)与双曲线C2的公共点左右焦点,它们在第一象限内交于点M,△MF1F2是以线段MF1为底边的等腰三角形,且|MF1|=2.若椭圆C1的离心率e=
,则双曲线C2的离心率是( )
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 8 |
A、
| ||
B、
| ||
C、
| ||
| D、4 |
在平面直角坐标系中,x轴的正半轴上有4个点,y轴的正半轴上有5个点,这9个点任意两点连线,则所有连线段的交点落入第一象限的个数最多是( )
| A、30 | B、60 |
| C、120 | D、240 |
已知双曲线C:
-
=1(a>0,b>0)的虚轴长是实轴长的2倍,则此双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||
| B、2 | ||
C、
| ||
D、
|
将5名实习教师分配到高一年级的3个班实习,每班至少1名,则不同的分配方案有( )
| A、30种 | B、60种 |
| C、90种 | D、150种 |
已知函数f(x)=2x2-bx(b∈R),则下列结论正确的是( )
| A、?b∈R,f(x)在(0,+∞)上是增函数 |
| B、?b∈R,f(x)在(0,+∞)上是减函数 |
| C、?b∈R,f(x)为奇函数 |
| D、?b∈R,f(x)为偶函数 |
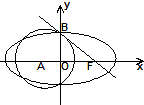 如图,已知点F为椭圆C:
如图,已知点F为椭圆C: