题目内容
已知函数f（x）=2x2-bx（b∈R），则下列结论正确的是（ ）
| A、?b∈R，f（x）在（0，+∞）上是增函数 |
| B、?b∈R，f（x）在（0，+∞）上是减函数 |
| C、?b∈R，f（x）为奇函数 |
| D、?b∈R，f（x）为偶函数 |
考点：二次函数的性质
专题：函数的性质及应用
分析：根据二次函数的图象和性质，分别进行判断即可得到结论．
解答：
解：函数的对称轴为x=b，∴函数在（-∞，b）上单调递减，在（b，+∞）上单调递增，
∴A，B错误．
当b=0时f（x）=2x2，为偶函数，当b≠0时，f（x）为非奇非偶函数，
∴C错误，D正确．
故选：D．
∴A，B错误．
当b=0时f（x）=2x2，为偶函数，当b≠0时，f（x）为非奇非偶函数，
∴C错误，D正确．
故选：D．
点评：本题主要考查二次函数的图象和性质，比较基础．
练习册系列答案
相关题目
下列函数中既是奇函数，又在区间[-1，1]上单调递减的函数是（ ）
| A、f（x）=|tan2x| | ||||||
| B、f（x）=-|x+1| | ||||||
C、f（x）=
| ||||||
D、f（x）=log
|
已知ω＞0，|φ|＜| π |
| 2 |
A、向右平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向左平移
|
在区间[0，1]上任取三个数x，y，z，若向量
=（x，y，z），则事件|
|≥1发生的概率是（ ）
| m |
| m |
A、
| ||
B、1-
| ||
C、1-
| ||
D、
|
现有10个数，它们能构成一个以1为首项，-3为公比的等比数列，若从这10个数中随机抽取一个数，则它小于8的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
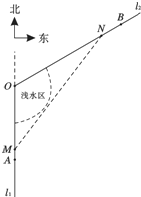某港湾的平面示意图如图所示，O，A，B分别是海岸线l1，l2上的三个集镇，A位于O的正南方向6km处，B位于O的北偏东60°方向10km处．