题目内容

将5名实习教师分配到高一年级的3个班实习，每班至少1名，则不同的分配方案有（　　）
A、30种B、60种
C、90种D、150种
考点：排列、组合的实际应用
专题：计算题
分析：根据题意，分两种情况讨论：①将5名教师分成三组，一组1人，另两组都是2人，②将5名教师分成三组，一组3人，另两组都是1人，由组合数公式计算可得每种情况下的分配方案数目，由分类计数原理计算可得答案．
解答： 解：将5名实习教师分配到高一年级的3个班实习，每班至少1名，有2种情况：
①将5名教师分成三组，一组1人，另两组都是2人，有
C
1
5
C
2
4
C
2
2
A
2
2
=15种分组方法，
再将3组分到3个班，共有15•A33=90种不同的分配方案，
②将5名教师分成三组，一组3人，另两组都是1人，有
C
3
5
C
1
2
C
1
1
A
2
2
=10种分组方法，
再将3组分到3个班，共有10•A33=60种不同的分配方案，
共有90+60=150种不同的分配方案，
故选：D．
点评：本题考查排列、组合的运用，注意先要根据题意要求，进行分类讨论，其次要正确运用分组公式．
练习册系列答案
相关题目
设[x]表示不超过实数x的最大整数，则方程[tanx]=2cos2x的解为
 
．
已知△ABC外接圆的半径为1，圆心为O，且
CA
+
BA
=2
OA
，|
OA
|=|
AB
|，则
CA
•
BC
的值是（　　）
A、3B、2C、-2D、-3
棱长均为3三棱锥S-ABC，若空间一点P满足
SP
=x
SA
+y
SB
+z
SC
（x+y+z=1）则|
SP
|的最小值为（　　）
A、
6
B、
6
3
C、
3
6
D、1
设a＞0，且a≠1，则“函数y=logax在（0，+∞）上是减函数”是“函数y=（2-a）x3在R上是增函数”的（　　）
A、充分而不必要条件
B、必要而不充分条件
C、充分必要条件
D、既不充分也不必要条件
设z=1-i（i是虚数单位），则复数
2
z
的虚部是（　　）
A、1B、-1C、iD、-i
平行四边形ABCD中，AB=1，AD=
2
，且∠BAD=45°，以BD为折线，把△ABD折起，使平面ABD⊥平面BCD，连接AC．

（Ⅰ）求证：AB⊥DC；
（Ⅱ）求二面角B-AC-D的大小．
某校研究性学习小组，为了分析2012年某小国的宏观经济形势，查阅了有关材料，得到2011年和2012年1-5月该国CPI同比（即当年某月与前一年同月比）的增长数据（见下表），但2012年3，4，5三个月的数据（分别记为x，y，z）没有查到，有的同学清楚记得2012年1-5月的CPI数据成等差数列．
（Ⅰ）求x，y，z的值；
（Ⅱ）求2012年1-5月该国CPI数据的方差；
（Ⅲ）一般认为，某月CPI达到或超过3个百分点就已经通货膨胀，而达到或超过5个百分点则严重通货膨胀．现随机的从下表2011年的五个月和2012年的五个月的数据中各抽取一个数据，求相同月份2011年通货膨胀，并且2012年严重通货膨胀的概率．附表：2011年和2012年1-5月CPI数据（单位：百分点 注：1个百分点=1%）
年份
月份		 1 2 3 4 5
2011 2.7 2.4 2.8 3.1 2.9
2012 4.9 5.0 x y z
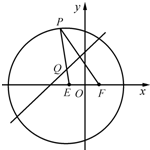如图，已知圆E：（x+1）2+y2=16，点F（1，0），P是圆E上任意一点．线段PF的垂直平分线和半径PE相交于Q．
（Ⅰ）求动点Q的轨迹Γ的方程；
（Ⅱ）点A（-2，0），B（2，0），点G是轨迹Γ上的一个动点，直线AG与直线x=2相交于点D，试判断以线段BD为直径的圆与直线GF的位置关系，并证明你的结论．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网