题目内容
现有10个数，它们能构成一个以1为首项，-3为公比的等比数列，若从这10个数中随机抽取一个数，则它小于8的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：古典概型及其概率计算公式
专题：概率与统计
分析：先由题意写出成等比数列的10个数为，然后找出小于8的项的个数，代入古典概论的计算公式即可求解
解答：
解：由题意成等比数列的10个数为：1，-3，（-3）2，（-3）3…（-3）9
其中小于8的项有：1，-3，（-3）3，（-3）5，（-3）7，（-3）9共6个数
这10个数中随机抽取一个数，
则它小于8的概率是P=
=
．
故选：C．
其中小于8的项有：1，-3，（-3）3，（-3）5，（-3）7，（-3）9共6个数
这10个数中随机抽取一个数，
则它小于8的概率是P=
| 6 |
| 10 |
| 3 |
| 5 |
故选：C．
点评：本题主要考查了等比数列的通项公式及古典概率的计算公式的应用，属于基础试题
练习册系列答案
教学练新同步练习系列答案
相关题目
对于定义在R上的函数f（x），以下四个命题中错误的是 （ ）
| A、若f（x）是奇函数，则f（x-2）的图象关于点A（2，0）对称 |
| B、若函数f（x-2）的图象关于直线x=2对称，则f（x）为偶函数 |
| C、若对x∈R，有f（x-2）=-f（x），则4是f（x）的周期 |
| D、函数y=f（x-2）与y=f（2-x）的图象关于直线x=0对称 |
各项均为实数的等比数列{an}中，a1=1，a5=4，则a3=（ ）
| A、2 | ||
| B、-2 | ||
C、
| ||
D、-
|
已知函数f（x）=2x2-bx（b∈R），则下列结论正确的是（ ）
| A、?b∈R，f（x）在（0，+∞）上是增函数 |
| B、?b∈R，f（x）在（0，+∞）上是减函数 |
| C、?b∈R，f（x）为奇函数 |
| D、?b∈R，f（x）为偶函数 |
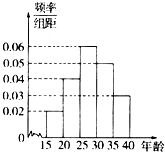山东省第二十三届运动会将于2014年9月16日在济宁市开幕，为办好省运会，济宁市计划招募各类志愿者1.2万人．为做好宣传工作，招募小组对济宁市15-40岁的人群随机抽取了100人，回答“省运会”的有关知识，根据统计结果制作了如下的统计图及表：
如图，平面ABB1A1为圆柱OO1的轴截面，点C为