Question

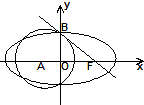如图，已知点F为椭圆C：

x2

a2

+

y2

b2

=1（a＞b＞0）右焦点，圆A：（x+t）²+y²=2（t＞0）与椭圆C的一个公共点为B（0，1），且直线FB与圆A相切于点B．
（Ⅰ）求t的值及椭圆C的标准方程；
（Ⅱ）设动点P（x₀，y₀）满足

OP

=

OM

+3

ON

，其中M、N是椭圆C上的点，O为原点，直线OM与ON的斜率之积为-

1

2

，求证：x₀²+2y₀²为定值．

Answer 1

考点：直线与圆锥曲线的综合问题

专题：综合题,圆锥曲线的定义、性质与方程

分析：（Ⅰ）根据圆A：（x+t）²+y²=2（t＞0）与椭圆C的一个公共点为B（0，1），求t的值；在Rt△AFB中，|AB|²+|FB|²=|AF|²，求出c，即可求出椭圆C的标准方程；
（Ⅱ）设M（x₁，y₁），N（x₂，y₂），利用

OP

=

OM

+3

ON

，可得x₀=x₁+3x₂，y₀=y₁+3y₂，利用直线OM与ON的斜率之积为-

1

2

，可得x₁x₂+2y₁y₂=0，从而可得x₀²+2y₀²为定值．

解答： 解：（Ⅰ）由题意可知b=1，
∵t²+1=2，∴t=±1．
∵t＞0，∴t=1．…..（2分）
在Rt△AFB中，|AB|²+|FB|²=|AF|²，
∴2+（1+c²）=（1+c）²，
∴c=1，a=

2

故椭圆的标准方程为：

x2

2

+y2=1…..（6分）
（Ⅱ）证明：设M（x₁，y₁），N（x₂，y₂），
∵

OP

=

OM

+3

ON

，
∴x₀=x₁+3x₂，y₀=y₁+3y₂
∵M、N在椭圆上，∴

x

2 1

+2

y

2 1

=2，

x

2 2

+2

y

2 2

=2
又直线OM与ON的斜率之积为-

1

2

，
∴x₁x₂+2y₁y₂=0，
于是x02+2y02=(x12+6x1x2+9x22)+2(y12+6y1y2+9y22)=(

x

2 1

+2

y

2 1

)+6(x1x2+2y1y2)+9(

x

2 2

+2

y

2 2

)=20．
故x02+2y02为定值．…..（13分）

点评：本题考查椭圆的标准方程，考查向量知识，考查学生的计算能力，属于中档题．