在一次抛硬币实验中,甲、乙两人各抛一枚硬币一次,设命题p是“甲抛的硬币正面向上”,q是“乙抛的硬币正面向上”,则命题“至少有一人抛的硬币是正面向下”可表示为( )
| A、(¬p)∨(¬q) |
| B、p∧(¬q) |
| C、(¬p)∧(¬q) |
| D、p∨q |
已知2a+b=t(a>0,b>0),t为常数,若ab的最大值为2时,a2+b2=( )
| A、2 | B、3 | C、4 | D、5 |
定义在R上的函数f(x)的图象既关于点(1,1)对称,又关于点(3,2)对称,则f(0)+f(2)+f(4)+…+f(18)=( )
| A、24 | B、32 | C、46 | D、50 |
已知随机变量ξ服从正态分布N(2,σ2),且P(ξ<4)=0.9,则P(0<ξ<2)=( )
| A、0.2 | B、0.3 |
| C、0.4 | D、0.6 |
若“0<x<1”是“(x-a)[x-(a+2)]≤0”的充分不必要条件,则a的取值范围是( )
| A、(-∞,0]∪[1,+∞) |
| B、(-1,0) |
| C、[-1,0] |
| D、(-∞,-1]∪[0,+∞) |
| ∫ | 2 -1 |
| A、0 | ||
B、
| ||
C、
| ||
| D、1 |
函数f(x)=x2sinx的图象大致为( )
A、 |
B、 |
C、 |
D、 |
若圆(x-3)2+(y+5)2=r2上的点到直线4x-3y-2=0的最近距离等于1,则半径r的值为( )
| A、4 | B、5 | C、6 | D、9 |
要得到函数g(x)=cos2x的图象,只需将f(x)=sin(2x+
)的图象( )
| 5π |
| 6 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
已知函数 f(x)=x2+x,执行如图所示的程序框图,若输出的结果是
,则判断框中的条件应是( )
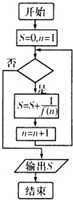
| 31 |
| 32 |

| A、n≤30 | B、n≤31 |
| C、n≤32 | D、n≤33 |