题目内容
若“0＜x＜1”是“（x-a）[x-（a+2）]≤0”的充分不必要条件，则a的取值范围是（ ）
| A、（-∞，0]∪[1，+∞） |
| B、（-1，0） |
| C、[-1，0] |
| D、（-∞，-1]∪[0，+∞） |
考点：必要条件、充分条件与充要条件的判断
专题：简易逻辑
分析：结合不等式的性质，利用充分条件和必要条件的定义进行判断即可得到结论．
解答：
解：∵（x-a）[x-（a+2）]≤0，
∴a≤x≤a+2，
若“0＜x＜1”是“（x-a）[x-（a+2）]≤0”的充分不必要条件，
则
，
即-1≤a≤0，
故选：C．
∴a≤x≤a+2，
若“0＜x＜1”是“（x-a）[x-（a+2）]≤0”的充分不必要条件，
则
|
即-1≤a≤0，
故选：C．
点评：本题主要考查充分条件和必要条件的判定，利用不等式的性质是解决本题的关键．
练习册系列答案
相关题目
已知函数 f（x）=x2+x，执行如图所示的程序框图，若输出的结果是
，则判断框中的条件应是（ ）
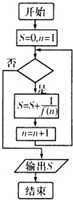
| 31 |
| 32 |
| A、n≤30 | B、n≤31 |
| C、n≤32 | D、n≤33 |
设向量
=（
，sinα），
=（cosα，
），且
∥
，则锐角α为（ ）
| a |
| 2 |
| 3 |
| b |
| 3 |
| 4 |
| a |
| b |
| A、30° | B、45° |
| C、60° | D、75° |
已知
=（1，2），
=（3，n），若
∥
，则n等于（ ）
| AB |
| CD |
| AB |
| CD |
| A、3 | B、4 | C、5 | D、6 |
设角α的终边过点P（-4，3），则2sinα+cosα的值为（ ）
A、
| ||||
B、
| ||||
C、-
| ||||
| D、以上都不正确 |
设复数z=
，则
=（ ）
| 2i |
| 1-i |
. |
| z |
| A、1+i | B、1-i |
| C、-1+i | D、-1-i |