题目内容
定义在R上的函数f(x)的图象既关于点(1,1)对称,又关于点(3,2)对称,则f(0)+f(2)+f(4)+…+f(18)=( )
| A、24 | B、32 | C、46 | D、50 |
考点:函数的值
专题:
分析:根据函数的对称性,即可得到结论.
解答:
解:由已知可得f(1-x)+f(1+x)=2,f(3-x)+f(3+x)=4,
∴f(x+4)-f(x)=2.
于是f(18)+f(16)=18,
f(14)+f(12)=14,f(10)+f(8)=10,
f(6)+f(4)=6,
f(2)+f(0)=2.
则累加得f(0)+f(2)+…+f(18)=2+6+10+14+18=50.
故选:D
巧解:由题意不妨设函数f(x)=
x+
,代入即可得到答案.
∴f(x+4)-f(x)=2.
于是f(18)+f(16)=18,
f(14)+f(12)=14,f(10)+f(8)=10,
f(6)+f(4)=6,
f(2)+f(0)=2.
则累加得f(0)+f(2)+…+f(18)=2+6+10+14+18=50.
故选:D
巧解:由题意不妨设函数f(x)=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题主要考查函数值的计算,根据函数的对称性得到函数关系式是解决本题的关键.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
为了得到函数y=
(sin2x-cos2x)的图象,只要把函数y=sin2x的图象上所有的点( )
| ||
| 2 |
A、向左平行移动
| ||
B、向右平行移动
| ||
C、向左平行移动
| ||
D、向右平行移动
|
若圆(x-3)2+(y+5)2=r2上的点到直线4x-3y-2=0的最近距离等于1,则半径r的值为( )
| A、4 | B、5 | C、6 | D、9 |
等比数列{an}中,a3=16,a4=8,则a1=( )
| A、64 | B、32 | C、4 | D、2 |
将5名学生分到A,B,C三个宿舍,每个宿舍至少1人至多2人,其中学生甲不到A宿舍的不同分法有( )
| A、18种 | B、36种 |
| C、48种 | D、60种 |
已知函数f(x)=cos(ωx+φ)(ω>0,|φ|≤
)的图象如图所示,则φ等于( )
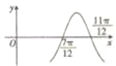
| π |
| 2 |

A、
| ||
B、
| ||
C、-
| ||
D、-
|
与30°角终边相同的角的集合是( )
| A、{θ|θ=30°+k•360°,k∈Z} |
| B、{θ|θ=30°+2k•360°,k∈Z} |
| C、{θ|θ=30°+k•180°,k∈Z} |
| D、{θ|θ=30°+k•90°,k∈Z} |