题目内容
在一次抛硬币实验中,甲、乙两人各抛一枚硬币一次,设命题p是“甲抛的硬币正面向上”,q是“乙抛的硬币正面向上”,则命题“至少有一人抛的硬币是正面向下”可表示为( )
| A、(¬p)∨(¬q) |
| B、p∧(¬q) |
| C、(¬p)∧(¬q) |
| D、p∨q |
考点:复合命题的真假
专题:简易逻辑
分析:利用“或”“且”“非”命题的意义即可得出.
解答:
解:¬P,表示“甲抛的硬币正面向下”,¬q表示“乙抛的硬币正面向下”.
则(¬p)∨(¬q)表示“至少有一人抛的硬币是正面向下”.
故选:A.
则(¬p)∨(¬q)表示“至少有一人抛的硬币是正面向下”.
故选:A.
点评:本题考查了“或”“且”“非”命题的意义,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
函数f(x)=
-
( )
| x |
| 1-2x |
| x |
| 2 |
| A、是偶函数,在(-∞,0)上是增函数 |
| B、是偶函数,在(-∞,0)上是减函数 |
| C、是奇函数,在(-∞,0)上是增函数 |
| D、是奇函数,在(-∞,0)上是减函数 |
| ∫ | 2 -1 |
| A、0 | ||
B、
| ||
C、
| ||
| D、1 |
已知P为△ABC所在平面内一点,当
+
=
时,点P位于△ABC的( )
| PA |
| PB |
| PC |
| A、AB边上 | B、BC边上 |
| C、内部 | D、外部 |
将函数f(x)=sin(2x-
)的图象向右平移
个单位所得到的一条对称轴的方程是( )
| π |
| 6 |
| π |
| 3 |
A、x=
| ||
B、x=
| ||
C、x=
| ||
| D、x=π |
在区间[-3,3]上任取两数x,y,使x2-y-1<0成立的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
函数f(x)=2|sinx|是( )
| A、最小正周期为2π的奇函数 |
| B、最小正周期为2π的偶函数 |
| C、最小正周期为π的奇函数 |
| D、最小正周期为π的偶函数 |

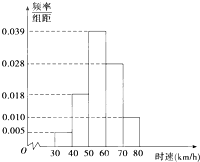 经过随机抽样获得100辆汽车经过某一雷达测速地区的时速(单位:km/h),并绘制成如图所示的频率分布直方图,其中这100辆汽车时速的范围是[30,80],数据分组为[30,40),[40,50),[50,60),[60,70),[70,80].设时速达到或超过60km/h的汽车有x辆,则x等于
经过随机抽样获得100辆汽车经过某一雷达测速地区的时速(单位:km/h),并绘制成如图所示的频率分布直方图,其中这100辆汽车时速的范围是[30,80],数据分组为[30,40),[40,50),[50,60),[60,70),[70,80].设时速达到或超过60km/h的汽车有x辆,则x等于