在△ABC中,若tanA•tanB>1,则△ABC的形状( )
| A、一定是锐角三角形 |
| B、一定是直角三角形 |
| C、一定是钝角三角形 |
| D、可能是锐角三角形,也可能是钝角三角形 |
一个四棱锥的三视图如图所示,则此四棱至的四个侧面中的最大面积是( )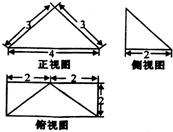

| A、3 | ||
B、2
| ||
| C、6 | ||
| D、8 |
已知函数f(x)=
,则下列结论错误的是( )
| sinx+cosx+|sinx-cosx| |
| 2 |
| A、f(x)的最小正周期是2π | ||||
B、f(x)的对称轴是x=
| ||||
C、f(x)的最小值是-
| ||||
D、f(x)在[
|
下列说法正确的是( )
| A、“a>b”是“a2>b2”的充分不必要条件 |
| B、命题“?x0∈R,x02+1<0”的否定是:“?x∈R,x2+1>0” |
| C、关于x的方程x2+(a+1)x+a-2=0的两根异号的充要条件是a<1 |
| D、若f(x)为R上的偶函数,则f(x-1)的图象关于直线x=1对称 |
设复数z1=1-ai,z2=(2+i)2(i为虚数单位),若复数
在复平面内对应的点在直线5x-5y+3=0上,则a=( )
| z1 |
| z2 |
| A、6 | B、-6 | C、-22 | D、22 |
若直线y=kx与圆(x-1)2+y2=1的两个交点关于直线x-y+b=0对称,则k,b的值分别为( )
| A、k=-1,b=1 |
| B、k=-1,b=-1 |
| C、k=1,b=1 |
| D、k=1,b=-1 |
已知直线x=
和点(
,0)恰好是函数f(x)=
sin(ωx+φ)图象的相邻的对称轴和对称中心,则f(x)的表达式可以是( )
| 5π |
| 12 |
| π |
| 6 |
| 2 |
A、f(x)=
| ||||
B、f(x)=
| ||||
C、f(x)=
| ||||
D、f(x)=
|
“x<0”是“ln(x+1)<0”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |