题目内容
若直线y=kx与圆(x-1)2+y2=1的两个交点关于直线x-y+b=0对称,则k,b的值分别为( )
| A、k=-1,b=1 |
| B、k=-1,b=-1 |
| C、k=1,b=1 |
| D、k=1,b=-1 |
考点:关于点、直线对称的圆的方程
专题:直线与圆
分析:由题意可得,圆心(1,0)在直线x-y+b=0上,由此求得得b的值;再根据直线y=kx与直线x-y+b=0垂直,可得k的值,从而得出结论.
解答:
解:由题意可得,圆心(1,0)在直线x-y+b=0上,∴1-0+b=0,解得b=-1.
再根据直线y=kx与直线x-y+b=0垂直,可得 k=-1,
故选:B.
再根据直线y=kx与直线x-y+b=0垂直,可得 k=-1,
故选:B.
点评:本题主要考查直线和圆的位置关系,两条直线垂直的性质,属于基础题.

练习册系列答案
相关题目
若集合A={-1,0},B={0,1},则A∩B=( )
| A、{0} |
| B、{-1,0} |
| C、{0,1} |
| D、{-1,0,1} |
| 2 |
| 1-i |
| A、1-i | B、1+i |
| C、2-i | D、2+i |
一个几何体的三视图如图所示(单位:cm),则该几何体的体积为( )


| A、1cm3 |
| B、2cm3 |
| C、3cm3 |
| D、4cm3 |
一个四棱锥的三视图如图所示,则此四棱至的四个侧面中的最大面积是( )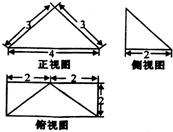

| A、3 | ||
B、2
| ||
| C、6 | ||
| D、8 |