对于定义域为D的函数y=f(x)和常数C,若对任意正实数ξ,存在x∈D,使得0<|f(x)-c|<ξ恒成立,则称函数y=f(x)为“敛C函数”.现给出如下函数:
①f(x)=x(x∈Z); ②f(x)=(
)x+1(x∈Z);③f(x)=log2x;
其中为“敛1函数”的有( )
①f(x)=x(x∈Z); ②f(x)=(
| 1 |
| 2 |
其中为“敛1函数”的有( )
| A、② | B、①③ | C、②③ | D、①③ |
已知圆x2-x+y2=6经过双曲线
-
=1(a,b>0)的左顶点和右焦点,则双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
| B、2 | ||||
C、
| ||||
D、
|
下列有关命题的说法正确的是( )
| A、命题“若x2=1,则x=1”是真命题 | ||||
| B、“x=-1”是“x2-5x-6=0”的必要不充分条件 | ||||
| C、命题“?x∈R使得x2+x+1<0”的否定是:“?x∈R,有x2+x+1>0” | ||||
D、命题“若x=
|
已知函数f(x)=(x-a)(x-b)+2,(a<b),若α,β(α<β)是方程f(x)=0的两个根,则实数a,b,α,β之间的大小关系是( )
| A、α<a<b<β |
| B、a<α<β<b |
| C、α<b<a<β |
| D、α<a<β<b |
已知△ABC中,角A,B,C的对边是a,b,c,且a,b,c成等比数列,则函数y=sinB+cosB的取值范围是( )
A、[-
| ||||
B、(1,
| ||||
C、[1,
| ||||
D、(0,
|
已知函数f(x)=
若直线y=m与函数f(x)的图象有两个不同的交点,则实数m的取值范围是( )
|
| A、m∈R | B、m>1 |
| C、m>0 | D、0<m<1 |
积分∫
dx=( )
0 |
| cos2x |
| cosx+sinx |
| A、-1 | ||
| B、0 | ||
| C、1 | ||
D、
|
已知数列{an}满足a1=1,a2=2,an+2=(1+cos2
)an+sin2
,则该数列的前18项和为( )
| nπ |
| 2 |
| nπ |
| 2 |
| A、2101 | B、2012 |
| C、1012 | D、1067 |
二次不等式ax2+bx+1>0的解集为{x|-1<x<
},则ab的值为( )
| 1 |
| 3 |
| A、-5 | B、5 | C、-6 | D、6 |
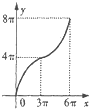
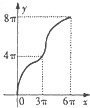
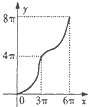
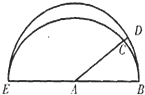 如图是半径为4的半圆A与它的内切半椭圆(长半轴长为4,短半轴长为3),AD为半圆的半径,且交半椭圆于点C.现AD绕着A点从AB所在的位置逆时针以1弧度/秒的速度旋转,设圆弧BD与AD、AB围成的面积为y,椭圆弧BC与AC、AB所围成的面积为x,则函数y=f(x)的图象大致是( )
如图是半径为4的半圆A与它的内切半椭圆(长半轴长为4,短半轴长为3),AD为半圆的半径,且交半椭圆于点C.现AD绕着A点从AB所在的位置逆时针以1弧度/秒的速度旋转,设圆弧BD与AD、AB围成的面积为y,椭圆弧BC与AC、AB所围成的面积为x,则函数y=f(x)的图象大致是( )