题目内容
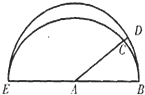 如图是半径为4的半圆A与它的内切半椭圆(长半轴长为4,短半轴长为3),AD为半圆的半径,且交半椭圆于点C.现AD绕着A点从AB所在的位置逆时针以1弧度/秒的速度旋转,设圆弧BD与AD、AB围成的面积为y,椭圆弧BC与AC、AB所围成的面积为x,则函数y=f(x)的图象大致是( )
如图是半径为4的半圆A与它的内切半椭圆(长半轴长为4,短半轴长为3),AD为半圆的半径,且交半椭圆于点C.现AD绕着A点从AB所在的位置逆时针以1弧度/秒的速度旋转,设圆弧BD与AD、AB围成的面积为y,椭圆弧BC与AC、AB所围成的面积为x,则函数y=f(x)的图象大致是( )A、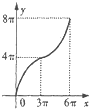 |
B、 |
C、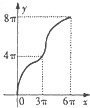 |
D、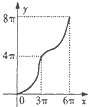 |
考点:函数的图象
专题:函数的性质及应用
分析:因为函数关系式不好求,所以可利用函数图象的变化趋势与AD绕A旋转的过程中,两个面积之间的相对变化关系来解决.
解答:
 解:如图,当AD绕着点A从B点沿着半圆弧逆时针匀速转到E的过程中,单位时间内扇形ABD的面积变化量不变,但单位时间内曲边三角形ABC的面积的增量越来越小,到AD转到与EB垂直时最小,也就相当于在单位时间内,扇形的面积相对于曲边三角形ABC的面积“增量”增大的越来越快,也就相当于扇形ABD之面积y相对于曲边三角形ABC的面积x增加的越来越快,到AD转到与EB垂直时最快,则y关于x的函数图象从O开始,自左向右,从“平缓”逐渐变得“陡峭”,到AD转到与EB垂直时最“陡”.当AD从与EB垂直
解:如图,当AD绕着点A从B点沿着半圆弧逆时针匀速转到E的过程中,单位时间内扇形ABD的面积变化量不变,但单位时间内曲边三角形ABC的面积的增量越来越小,到AD转到与EB垂直时最小,也就相当于在单位时间内,扇形的面积相对于曲边三角形ABC的面积“增量”增大的越来越快,也就相当于扇形ABD之面积y相对于曲边三角形ABC的面积x增加的越来越快,到AD转到与EB垂直时最快,则y关于x的函数图象从O开始,自左向右,从“平缓”逐渐变得“陡峭”,到AD转到与EB垂直时最“陡”.当AD从与EB垂直
转到AE位置时,y随着x的变化趋势和刚才正好相反,其图象又逐渐从“陡峭”变得“平缓”.
故选B
 解:如图,当AD绕着点A从B点沿着半圆弧逆时针匀速转到E的过程中,单位时间内扇形ABD的面积变化量不变,但单位时间内曲边三角形ABC的面积的增量越来越小,到AD转到与EB垂直时最小,也就相当于在单位时间内,扇形的面积相对于曲边三角形ABC的面积“增量”增大的越来越快,也就相当于扇形ABD之面积y相对于曲边三角形ABC的面积x增加的越来越快,到AD转到与EB垂直时最快,则y关于x的函数图象从O开始,自左向右,从“平缓”逐渐变得“陡峭”,到AD转到与EB垂直时最“陡”.当AD从与EB垂直
解:如图,当AD绕着点A从B点沿着半圆弧逆时针匀速转到E的过程中,单位时间内扇形ABD的面积变化量不变,但单位时间内曲边三角形ABC的面积的增量越来越小,到AD转到与EB垂直时最小,也就相当于在单位时间内,扇形的面积相对于曲边三角形ABC的面积“增量”增大的越来越快,也就相当于扇形ABD之面积y相对于曲边三角形ABC的面积x增加的越来越快,到AD转到与EB垂直时最快,则y关于x的函数图象从O开始,自左向右,从“平缓”逐渐变得“陡峭”,到AD转到与EB垂直时最“陡”.当AD从与EB垂直转到AE位置时,y随着x的变化趋势和刚才正好相反,其图象又逐渐从“陡峭”变得“平缓”.
故选B
点评:这个题的解析式不容易求出来,实际上考查的是,函数图象的变化趋势与实际问题的量的变化之间的关系,主要是看他们在相同的时间差相对变化的快慢.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
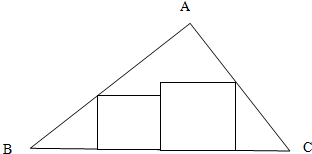
现有等腰三角形纸片ABC,∠A=90°,BC=2,按图示方式剪下两个正方形,则这两个正方形的面积之和的最小值为( )

A、
| ||||
B、
| ||||
C、
| ||||
D、
|
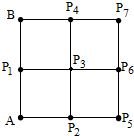 如图,四个边长为1的小正方形排成一个大正方形,AB是大正方形的一条边,Pi(i=1,2,…,7)是小正方形的其余顶点,则
如图,四个边长为1的小正方形排成一个大正方形,AB是大正方形的一条边,Pi(i=1,2,…,7)是小正方形的其余顶点,则| AB |
| APi |
| A、7 | B、5 | C、3 | D、1 |
已知△ABC中,角A,B,C的对边是a,b,c,且a,b,c成等比数列,则函数y=sinB+cosB的取值范围是( )
A、[-
| ||||
B、(1,
| ||||
C、[1,
| ||||
D、(0,
|
 如图,PQ是半径为1的圆A的直径,△ABC是边长为1的正三角形,则
如图,PQ是半径为1的圆A的直径,△ABC是边长为1的正三角形,则| BP |
| CQ |
A、
| ||
B、
| ||
| C、1 | ||
| D、2 |
若3a,b,c成等比数列,则函数f(x)=ax3+bx2+cx+d的零点个数为( )
| A、0 | B、1 | C、2 | D、3 |