题目内容
对于定义域为D的函数y=f(x)和常数C,若对任意正实数ξ,存在x∈D,使得0<|f(x)-c|<ξ恒成立,则称函数y=f(x)为“敛C函数”.现给出如下函数:
①f(x)=x(x∈Z); ②f(x)=(
)x+1(x∈Z);③f(x)=log2x;
其中为“敛1函数”的有( )
①f(x)=x(x∈Z); ②f(x)=(
| 1 |
| 2 |
其中为“敛1函数”的有( )
| A、② | B、①③ | C、②③ | D、①③ |
考点:函数的值域
专题:新定义,函数的性质及应用
分析:由“敛C函数”的定义可知,当自变量x趋近于某个值或无穷大时,函数值y无限趋近于一个常数C,由此性质对三个函数逐一判断
解答:
解:对于函数①f(x)=x,取ξ=
,因为x∈Z,找不到x,使得0<|x-1|<
成立,所以函数①不是“敛1函数”;
对于函数②f(x)=(
)x+1(x∈z),当x→+∞时,(
)x→0,所以,(
) x+1→1,对任意正实数ξ,总能找到一个足够大的正整数x,
使得0<|f(x)-1|<ξ,故函数②是“敛1函数
对于函数③f(x)=log2x,当x→2时,log2x→log22=1,所以对于无论多大或多小的正数ξ,总会找到一个x,使得0<|f(x)-1|<ξ成立
故函数③是“敛1函数”;
故选C
| 1 |
| 2 |
| 1 |
| 2 |
对于函数②f(x)=(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
使得0<|f(x)-1|<ξ,故函数②是“敛1函数
对于函数③f(x)=log2x,当x→2时,log2x→log22=1,所以对于无论多大或多小的正数ξ,总会找到一个x,使得0<|f(x)-1|<ξ成立
故函数③是“敛1函数”;
故选C
点评:本题主要是考查对“敛C函数”的定义准确理解,属于中档题

练习册系列答案
相关题目
已知
+
=1(a>b>0),M,N是椭圆的左、右顶点,P是椭圆上任意一点,且直线PM、PN的斜率分别为k1,k2(k1,k2≠0),若|k1|+|k2|的最小值为1,则椭圆的离心率为 .
| x2 |
| a2 |
| y2 |
| b2 |
若a>0,b>0,则不等式-b<
<a的解集为( )
| 1 |
| x |
A、{x|-
| ||||
B、{x|-
| ||||
C、{x|x<-
| ||||
D、{x|x<-
|
已知双曲线C:
-
=1(a>0,b>0)离心率为3,直线y=2与双曲线C的两个交点间的距离为
,则双曲线C的方程是( )
| x2 |
| a2 |
| y2 |
| b2 |
| 6 |
| A、2x2-y2=1 | ||||
B、x2-
| ||||
C、
| ||||
D、
|
已知函数f(x)=
若直线y=m与函数f(x)的图象有两个不同的交点,则实数m的取值范围是( )
|
| A、m∈R | B、m>1 |
| C、m>0 | D、0<m<1 |
等差数列前n项和为Sn,若a4+a7+a13=30,则S15的值是( )
| A、150 | B、65 | C、70 | D、75 |
双曲线
-
=1的离心率的值为( )
| y2 |
| 4 |
| x2 |
| 5 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
执行如图所示的程序框图,若输入a1=2,a2=0,a3=1,a4=4,则计算机输出的结果是( )


| A、2 | B、0 | C、1 | D、4 |
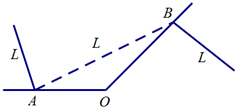 如图,某城市有一条公路从正西方AO通过市中心O后转向东北方OB,现要修筑一条铁路L,L在OA上设一站A,在OB上设一站B,铁路在AB部分为直线段,为了市民出行方便与城市环境问题,现要求市中心O到AB的距离为10km,设∠OAB=α.
如图,某城市有一条公路从正西方AO通过市中心O后转向东北方OB,现要修筑一条铁路L,L在OA上设一站A,在OB上设一站B,铁路在AB部分为直线段,为了市民出行方便与城市环境问题,现要求市中心O到AB的距离为10km,设∠OAB=α.