题目内容
已知圆x2-x+y2=6经过双曲线
-
=1(a,b>0)的左顶点和右焦点,则双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
| B、2 | ||||
C、
| ||||
D、
|
考点:双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:首先把圆的一般方程转化为一般方程,求出圆心的坐标和半径的长,再根据圆心到双曲线
-
=1(a,b>0)的左顶点和右焦点的距离相等,求出a,c,最后根据离心率公式求得.
| x2 |
| a2 |
| y2 |
| b2 |
解答:
解:∵x2-x+y2=6,
∴(x-
)2+y2=(
)2
∴圆心坐标为(
,0),半径为
,
又圆x2-x+y2=6经过双曲线
-
=1(a,b>0)的左顶点和右焦点,
∴左顶点和右焦点的坐标为(-a,0),(c,0),
∴a+
=
,c-
=
解得a=2,c=3
故双曲线的离心率e=
=
.
故选:A.
∴(x-
| 1 |
| 2 |
| 5 |
| 2 |
∴圆心坐标为(
| 1 |
| 2 |
| 5 |
| 2 |
又圆x2-x+y2=6经过双曲线
| x2 |
| a2 |
| y2 |
| b2 |
∴左顶点和右焦点的坐标为(-a,0),(c,0),
∴a+
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
解得a=2,c=3
故双曲线的离心率e=
| c |
| a |
| 3 |
| 2 |
故选:A.
点评:本题考查了圆的一般方程和标注方程之间的转化和双曲线的离心率的求法.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
给出如下四个命题:
①若“p∨q”为真命题,则p、q均为真命题;
②“若a>b,则2a>2b-1”的否命题为“若a≤b,则2a≤2b-1”;
③“?x∈R,x2+x≥1”的否定是“?x0∈R,x02+x0≤1”;
④“x>0”是“x+
≥2”的充要条件.
其中不正确的命题是( )
①若“p∨q”为真命题,则p、q均为真命题;
②“若a>b,则2a>2b-1”的否命题为“若a≤b,则2a≤2b-1”;
③“?x∈R,x2+x≥1”的否定是“?x0∈R,x02+x0≤1”;
④“x>0”是“x+
| 1 |
| x |
其中不正确的命题是( )
| A、①② | B、②③ | C、①③ | D、③④ |
积分∫
dx=( )
0 |
| cos2x |
| cosx+sinx |
| A、-1 | ||
| B、0 | ||
| C、1 | ||
D、
|
已知三棱锥的底面是边长为
的等边三角形,侧棱长都为2,则侧棱与底面所成角的大小为( )
| 3 |
| A、30° | B、45° |
| C、60° | D、90° |
在数列{an}中,a1=1,a2=
,且
+
=
(n≥3,n∈N*),则a4=( )
| 2 |
| 3 |
| 1 |
| an-2 |
| 1 |
| an |
| 2 |
| an-1 |
A、
| ||
B、
| ||
C、
| ||
D、-
|
设函数f(x)=x2-2ax+b(a,b∈R),则“f(x)=0在区间[1,2]有两个不同的实根”是“1<a<2”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
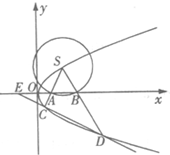 如图,S(1,1)是抛物线为y2=2px(p>0)上的一点,以S为圆心,r为半径(1<r<
如图,S(1,1)是抛物线为y2=2px(p>0)上的一点,以S为圆心,r为半径(1<r<