题目内容
已知△ABC中，角A，B，C的对边是a，b，c，且a，b，c成等比数列，则函数y=sinB+cosB的取值范围是（ ）
A、[-
| ||||
B、（1，
| ||||
C、[1，
| ||||
D、（0，
|
考点：余弦定理
专题：三角函数的求值
分析：根据a，b，c成等比数列，利用等比数列性质列出关系式，再利用余弦定理表示出cosB，将得出关系式代入，并利用基本不等式求出cosB的范围，进而求出B的范围，函数解析式利用两角和与差的正弦函数公式化简，根据正弦函数的值域即可确定出范围．
解答：
解：∵a，b，c成等比数列，∴b2=ac，
由余弦定理得：cosB=
=
≥
=
，
∴B∈（0，
]，即B+
∈（
，
]，
∴
＜sin（B+
）≤1，
函数y=sinB+cosB=
sin（B+
）∈（1，
]，
故选：B．
由余弦定理得：cosB=
| a2+c2-b2 |
| 2ac |
| a2+c2-ac |
| 2ac |
| 2ac-ac |
| 2ac |
| 1 |
| 2 |
∴B∈（0，
| π |
| 3 |
| π |
| 4 |
| π |
| 4 |
| 7π |
| 12 |
∴
| ||
| 2 |
| π |
| 4 |
函数y=sinB+cosB=
| 2 |
| π |
| 4 |
| 2 |
故选：B．
点评：此题考查了余弦定理，等比数列的性质，两角和与差的正弦函数公式，以及正弦函数的定义域与值域，熟练掌握定理及公式是解本题的关键．
练习册系列答案
相关题目
下列说法正确的是（ ）
A、若a∈R，则“
| ||
| B、“p∧q为真命题”是“p∨q为真命题”的必要不充分条件 | ||
C、若命题p：“?x∈R，sinx+cosx≤
| ||
| D、命题“?x0∈R，使得x02+2x0+3＜0”的否定是“?x∈R，x2+2x+3＞0” |
已知曲线C为三次函数f（x）=3x-x3的图象，过点M（2，1）作曲线C的切线，可能的切线条数是（ ）
| A、0 | B、1 | C、2 | D、3 |
设集合M={y|y=2sinx，x∈[-
，
]}，N={x|y=log2（x-1）}，则M∩N=（ ）
| π |
| 2 |
| π |
| 2 |
| A、{x|1＜x≤5} |
| B、{x|-1＜x≤0} |
| C、{x|-2≤x≤0} |
| D、{x|1＜x≤2} |
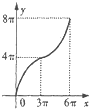
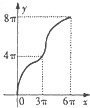
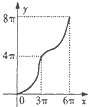
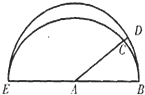如图是半径为4的半圆A与它的内切半椭圆（长半轴长为4，短半轴长为3），AD为半圆的半径，且交半椭圆于点C．现AD绕着A点从AB所在的位置逆时针以1弧度/秒的速度旋转，设圆弧BD与AD、AB围成的面积为y，椭圆弧BC与AC、AB所围成的面积为x，则函数y=f（x）的图象大致是（ ）
椭圆x2+4y2=36的一条弦被A（4，2）平分，那么这条弦所在的直线方程是（ ）
| A、x-2y=0 |
| B、2x+y-10=0 |
| C、x+2y-8=0 |
| D、2x-y-2=0 |
设等差数列{an}的通项公式满足an=2n-7（n∈N*），则|a1|+|a2|+…+|a15|=（ ）
| A、130 | B、139 |
| C、153 | D、178 |