题目内容
已知函数f(x)=(x-a)(x-b)+2,(a<b),若α,β(α<β)是方程f(x)=0的两个根,则实数a,b,α,β之间的大小关系是( )
| A、α<a<b<β |
| B、a<α<β<b |
| C、α<b<a<β |
| D、α<a<β<b |
考点:二次函数的性质
专题:函数的性质及应用
分析:由二次函数图象的特点和平移规律作图可得.
解答:
解:设y=(x-a)(x-b)的大致图象如图所示的抛物线①(黑色),
它与x轴的交点坐标的横坐标依次为a、b,
∴f(x)=(x-a)(x-b)+是由抛物线①向上平移个单位长度得到的.
如图中的抛物线②(红色),它与x轴的交点横坐标分别是α,β,
∴由图象得a<α<β<b
故选B

它与x轴的交点坐标的横坐标依次为a、b,
∴f(x)=(x-a)(x-b)+是由抛物线①向上平移个单位长度得到的.
如图中的抛物线②(红色),它与x轴的交点横坐标分别是α,β,
∴由图象得a<α<β<b
故选B

点评:本题考查二次函数的图象性质,二次函数图象的平移及二次函数的图象与x轴的交点坐标的特征是解决问题的关键,属中档题.

练习册系列答案
相关题目
小乐与小波在学了变量的相关性之后,两人约定回家去利用自己各自记录的6-10岁的身高记录作为实验数据,进行回归分析,探讨年龄x(岁)与身高y(cm)之间的线性相关性.经计算小乐与小波求得的线性回归直线分别为l1,l2,在认真比较后,两人发现他们这五年身高的平均值都为110cm,而且小乐的五组实验数据均满足所求的直线方程,小波则只有两组实验数据满足所求直线方程.下列说法错误的是( )
| A、直线l1,l2一定有公共点(8,110) |
| B、在两人的回归分析中,小乐求得的线性相关系数r=1,小波求得的线性相关系数r∈(0,1) |
| C、在小乐的回归分析中,他认为x与y之间完全线性相关,所以自己的身高y(cm)与年龄x(岁)成一次函数关系,利用l1可以准确预测自己20岁的身高 |
| D、在小波的回归分析中,他认为x与y之间不完全线性相关,所以自己的身高y(cm)与年龄x(岁)成相关关系,利用l2只可以估计预测自己20岁的身高 |
二次不等式ax2+bx+1>0的解集为{x|-1<x<
},则ab的值为( )
| 1 |
| 3 |
| A、-5 | B、5 | C、-6 | D、6 |
已知函数f(x)满足f(x+1)=
+f(x)(x∈R),且f(1)=
,则数列{f(n)}(n∈N*)前20项的和为( )
| 3 |
| 2 |
| 5 |
| 2 |
| A、305 | B、315 |
| C、325 | D、335 |
双曲线
-
=1的左、右焦点为F1,F2,直线x=
与双曲线的渐近线交于点P,过点P且与x轴平行的直线交双曲线右支于点M,过点M做x轴的垂线,垂足为N,若
=3
,则双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| a |
| 2 |
| F1N |
| NF2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
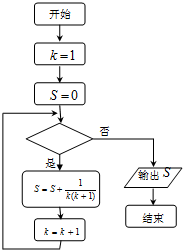
如果执行如图的程序框图,那么输出的S=
,那么判断框内是( )
| 2013 |
| 2014 |

| A、k≤2013? |
| B、k≤2014? |
| C、k≥2013? |
| D、k≥2014? |