设椭圆

x2

2

+

y2

m

=1和双曲线

y2

3

-x2=1的公共焦点分别为F₁、F₂，P为这两条曲线的一个交点，则cos∠F₁PF₂的值为（　　）

将正方体（如图）截去两个三棱锥，得到如图所示的几何体，则该几何体的主视图为（　　）

给出下列四个命题：
①直线垂直于一个平面内的无数条直线是这条直线与这个平面垂直的充要条件；
②过空间一定点有且只有一条直线与已知平面垂直；
③不在一个平面内的一条直线和平面内的一条直线平行是这条直线和这个平面平行的充分条件；
④一个二面角的两个半平面分别垂直于另一个二面角的两个半平面，则这两个二面角相等或互补．
其中真命题的为（　　）

若函数f（x）=x³-ax²+4在（0，2）内单调递减，则实数a的取值范围为（　　）

已知函数f（x）满足：①定义域为R；②对任意x∈R，都有f（x+2）=2f（x）；③当x∈[-1，1]时f（x）=-|x|+1．则方程f（x）=log₄|x|在区间[-7，7]内的解个数是（　　）

已知a＞0，设p：存在a∈R，使y=a^x是R上的单调递减函数； q：存在a∈R，使函数g（x）=lg（2ax²+2x+1）的值域为R，如果“p∧q”为假，“p∨q”为真，则a的取值范围是（　　）

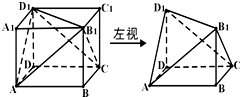
已知正四棱锥O-ABCD中，OA=AB，则OA与底面ABCD所成角的正弦值等于（　　）

函数y=x-lnx的单调增区间为（　　）

设F₁，F₂是双曲线

x2

a2

-

y2

b2

=1（a＞0，b＞0）的左、右焦点，过F₂与双曲线的一条渐近线平行的直线交另一条渐近线于点M，若点M在以F₁F₂为直径的圆上，则双曲线的离心率为（　　）

已知双曲线

x2

a2

-

y2

b2

=1的左、右焦点分别为F₁、F₂，过F₁作圆x²+y²=a²的切线分别交双曲线的左、右两支于点B、C，且|BC|=|CF₂|，则双曲线的渐近线方程为（　　）