Question

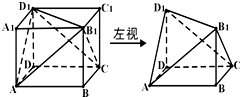
已知正四棱锥O-ABCD中，OA=AB，则OA与底面ABCD所成角的正弦值等于（　　）

• A、

  1

  2

• B、

  3

  3

• C、

  2

  2

• D、

  1

  3

Answer 1

考点：直线与平面所成的角

专题：计算题,空间角

分析：设O在底面ABCD中的射影为O′，则O′为底面ABCD的中心，求出O′A，OO′，即可求出OA与底面ABCD所成角的正弦值．

解答： 解：设O在底面ABCD中的射影为O′，则O′为底面ABCD的中心，O′A=

2

2

AB．
∵OA=AB，
∴OO′=

2

2

AB，
∴OA与底面ABCD所成角的正弦值等于

2

2

．
故选：C．

点评：本题考查直线与平面所成的角，考查学生的计算能力，比较基础．