题目内容
设椭圆
+
=1和双曲线
-x2=1的公共焦点分别为F1、F2,P为这两条曲线的一个交点,则cos∠F1PF2的值为( )
| x2 |
| 2 |
| y2 |
| m |
| y2 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、-
|
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:由双曲线
-x2=1得焦点为F1(0,-2),F 2 (0,2),解得m=6,由椭圆与双曲线的定义,得|PF1|+|PF2|=2
,|PF1|-|PF2|=±2
,由此得到2(|PF1|2+|PF2|2)=36,4|PF1|•|PF2|=12,再由余弦定理,能求出cos∠F1PF2.
| y2 |
| 3 |
| 6 |
| 3 |
解答:
解:由双曲线
-x2=1得焦点为F1(0,-2),F 2 (0,2),
∴m-2=4,解得m=6,
由椭圆与双曲线的定义,得:
|PF1|+|PF2|=2
,|PF1|-|PF2|=±2
,
两式分别平方后,相加得 2(|PF1|2+|PF2|2)=36,
两式分别平方后相减,得 4|PF1|•|PF2|=12,
因此,由余弦定理,得
cos∠F1PF2=(|PF1|2+|PF2|2-|F1F2|2)÷(2|PF1|•|PF2|)
=(18-16)÷6
=
.
故选:B.
| y2 |
| 3 |
∴m-2=4,解得m=6,
由椭圆与双曲线的定义,得:
|PF1|+|PF2|=2
| 6 |
| 3 |
两式分别平方后,相加得 2(|PF1|2+|PF2|2)=36,
两式分别平方后相减,得 4|PF1|•|PF2|=12,
因此,由余弦定理,得
cos∠F1PF2=(|PF1|2+|PF2|2-|F1F2|2)÷(2|PF1|•|PF2|)
=(18-16)÷6
=
| 1 |
| 3 |
故选:B.
点评:本题考查角的余弦值的求法,是中档题,解题时要注意审题,注意椭圆、双曲线的简单性质的灵活运用,注意余弦定理的合理运用.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
一个棱锥的三视图如图,则该棱锥的表面积为( )


A、48+12
| ||
B、48+24
| ||
C、72+12
| ||
D、72+24
|
已知a>0,设p:存在a∈R,使y=ax是R上的单调递减函数; q:存在a∈R,使函数g(x)=lg(2ax2+2x+1)的值域为R,如果“p∧q”为假,“p∨q”为真,则a的取值范围是( )
A、(
| ||
B、(
| ||
C、(0,
| ||
D、(0,
|
已知命题p:f(x)=
e-x在(0,+∞)上单调递减;命题q:双曲线
-
=1的焦点到抛物线x2=
y的准线的距离为2,则下列命题正确的是( )
| 1 | ||
|
| x2 |
| 4 |
| y2 |
| 5 |
| 1 |
| 4 |
| A、p∨q | B、p∧q |
| C、¬p∧q | D、¬p∨q |
直线l1:x+y-2
=0与直线l2:
(t为参数)的交点到原点O的距离是( )
| 2 |
|
| A、1 | ||
B、
| ||
| C、2 | ||
D、2
|
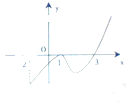 如图是函数y=f(x)的导函数y=f′(x)的图象,给出下列命题:
如图是函数y=f(x)的导函数y=f′(x)的图象,给出下列命题: 如图是某几何体的三视图,它的正视图和侧视图均为矩形,俯视图为正三角形(长度单位:cm)
如图是某几何体的三视图,它的正视图和侧视图均为矩形,俯视图为正三角形(长度单位:cm)