题目内容

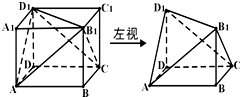
将正方体（如图）截去两个三棱锥，得到如图所示的几何体，则该几何体的主视图为（　　）
A、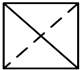
B、
C、
D、
考点：简单空间图形的三视图
专题：空间位置关系与距离
分析：正视图是从前向后看得到的视图，结合选项即可作出判断．
解答： 解：正视图是从前向后看得到的视图，几何体的轮廓是正方形，AB1是实线，D1C是虚线，结合选可知B符合．
故选：B．
点评：本题考查了简单组合体的三视图，属于基础题，关键掌握正视图是从前向后看得到的视图．
练习册系列答案
相关题目
若F1，F2是双曲线
x2
4
-y2=1的左，右焦点，点P是该双曲线的顶点，则|PF1|-|PF2|=
 
．
已知某个几何体是三视图（单位：cm）如图所示，则这个几何体的体积是
 
cm3．
偶函数f（x）满足f（x-1）=f（x+1），且在x∈[0，1]时，f（x）=x2，则关于x的方程f（x）=(
1
10
)|x|在[-2，3]上的根的个数是（　　）
A、3B、4C、5D、6
已知正四棱锥O-ABCD中，OA=AB，则OA与底面ABCD所成角的正弦值等于（　　）
A、
1
2
B、
3
3
C、
2
2
D、
1
3
如果对x＞0，y＞0，有f（x，y）=（x+4y）（
2
x
+
1
2y
）≥m恒成立，那么实数m的取值范围是（　　）
A、（-∞，4]
B、（8，+∞）
C、（-∞，0）
D、（-∞，8]
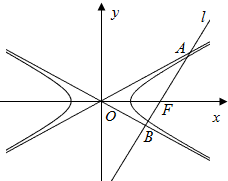如图所示，已知双曲线
x2
a2
-
y2
b2
=1（a＞b＞0）的右焦点为F，过F的直线l交双曲线的渐近线于A、B两点，且直线l的倾斜角是渐近线OA倾斜角的2倍，若
AF
=2
FB
，则该双曲线的离心率为（　　）
A、
3
2
4
B、
2
3
3
C、
30
5
D、
5
2
已知a、b、c分别是△ABC的三个内角A、B、C所对的边；
（1）若△ABC面积S△ABC=
3
2
，c=2，A=60°，求a、b的值；
（2）若sinA=2cosBsinC试判断△ABC的形状．
已知直三棱柱ABC-A′B′C′的各顶点都在同一球面，AB=2，AC=AA′=3，BC=4，求该球的体积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网