题目内容
若函数f(x)=x3-ax2+4在(0,2)内单调递减,则实数a的取值范围为( )
| A、[3,+∞) |
| B、{3} |
| C、(-∞,3] |
| D、(0,3) |
考点:利用导数研究函数的单调性
专题:导数的概念及应用
分析:求出导函数,令导函数小于等于0在(0,2)内恒成立,分离出参数a,求出函数的范围,得到a的范围.
解答:
解解:∵函数f(x)=x3-ax2+4在(0,2)内单调递减,
∴f′(x)=3x2-2ax≤0在(0,2)内恒成立,
即 a≥
x在(0,2)内恒成立,
∵
x<3
∴a≥3,
故选A.
∴f′(x)=3x2-2ax≤0在(0,2)内恒成立,
即 a≥
| 3 |
| 2 |
∵
| 3 |
| 2 |
∴a≥3,
故选A.
点评:解决函数在区间上的单调性已知求参数的范围的问题,递增时令导函数大于等于0恒成立;递减时,令导数小于等于0恒成立.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
设随机变量X~N(μ,σ2),则η=ax+b服从( )
| A、N(μ,σ2) | ||||
| B、N(aμ+b,a2σ2) | ||||
| C、N(0,1) | ||||
D、N(
|
设F1,F2是双曲线
-
=1(a>0,b>0)的左、右焦点,过F2与双曲线的一条渐近线平行的直线交另一条渐近线于点M,若点M在以F1F2为直径的圆上,则双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||
B、
| ||
| C、2 | ||
D、
|
正方体ABCD-A1B1C1D1中,M、N分别是棱DD1和BB1上的点,MD=
DD1,NB=
BB1,那么正方体的过M、N、C1的截面图形是( )
| 1 |
| 3 |
| 1 |
| 3 |
| A、三角形 | B、四边形 |
| C、五边形 | D、六边形 |
在极坐标系中,圆ρ=2sinθ的圆心到极轴的距离为( )
| A、1 | ||
B、
| ||
C、
| ||
| D、2 |
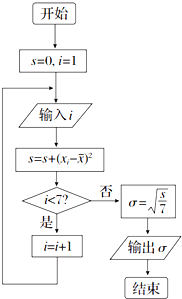 在2012~2013赛季NBA季后赛中,当一个球队进行完7场比赛被淘汰后,某个篮球爱好者对该队的7场比赛得分情况进行统计,如表:
在2012~2013赛季NBA季后赛中,当一个球队进行完7场比赛被淘汰后,某个篮球爱好者对该队的7场比赛得分情况进行统计,如表: