题目内容
已知函数f（x）满足：①定义域为R；②对任意x∈R，都有f（x+2）=2f（x）；③当x∈[-1，1]时f（x）=-|x|+1．则方程f（x）=log4|x|在区间[-7，7]内的解个数是（ ）
| A、10 | B、9 | C、8 | D、12 |
考点：抽象函数及其应用
专题：计算题,函数的性质及应用
分析：令-3≤x≤-1则-1≤x+2≤1，由f（x+2）=2f（x），求出f（x），同理求出-5≤x≤-3、-7≤x≤-5、1≤x≤3、3≤x≤5、5≤x≤7的函数f（x）的解析式，并画出图象，再画出y=log4|x|的图象，观察得出交点个数，即为方程解的个数．
解答：
解：令-3≤x≤-1则-1≤x+2≤1，
∵f（x+2）=2f（x），∴f（x）=
（1-|x+2|）（-3≤x≤-1）①
令-5≤x≤-3则-1≤x+4≤1，f（x+4）=1-|x+4|，又f（x+4）=2f（x+2）=4f（x），
∴f（x）=
（1-|x+4|）（-5≤x≤-3）②
则-7≤x≤-5时，f（x）=
（1-|x+6|）③
当1≤x≤3时，-1≤x-2≤1，f（x-2）=1-|x-2|
又f（x-2）=
f（x），即f（x）=2（1-|x-2|），
同理3≤x≤5时，
f（x）=4（1-|x-4|）④
当5≤x≤7时，f（x）=8（1-|x-6|）⑤
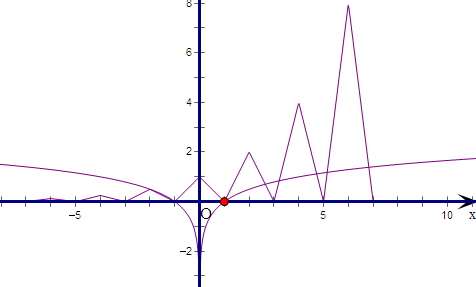
如图所示f（x）的图象，
再画出y=log4|x|的图象，观察得出交点数为8，
即方程f（x）=log4|x|在区间[-7，7]内的解个数是8．
故选：C．
解：令-3≤x≤-1则-1≤x+2≤1，∵f（x+2）=2f（x），∴f（x）=
| 1 |
| 2 |
令-5≤x≤-3则-1≤x+4≤1，f（x+4）=1-|x+4|，又f（x+4）=2f（x+2）=4f（x），
∴f（x）=
| 1 |
| 4 |
则-7≤x≤-5时，f（x）=
| 1 |
| 8 |
当1≤x≤3时，-1≤x-2≤1，f（x-2）=1-|x-2|
又f（x-2）=
| 1 |
| 2 |
同理3≤x≤5时，
f（x）=4（1-|x-4|）④
当5≤x≤7时，f（x）=8（1-|x-6|）⑤
如图所示f（x）的图象，
再画出y=log4|x|的图象，观察得出交点数为8，
即方程f（x）=log4|x|在区间[-7，7]内的解个数是8．
故选：C．
点评：本题考查函数的解析式的求法，函数的零点个数，以及函数的图象的画法，考查数形结合的思想方法．
练习册系列答案
相关题目
双曲线
-
=1（a＞0，b＞0）的左、右焦点分别为F1（-c，0），F2（c，0）．若双曲线上存在点P使
=
，则该双曲线的离心率的取值范围为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| sin∠PF1F2 |
| sin∠PF2F1 |
| a |
| c |
A、（1，
| ||||
| B、（1，2） | ||||
C、（1，
| ||||
D、（1，
|
已知双曲线
-
=1的左、右焦点分别为F1、F2，过F1作圆x2+y2=a2的切线分别交双曲线的左、右两支于点B、C，且|BC|=|CF2|，则双曲线的渐近线方程为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| A、y=±3x | ||
| B、y=±2x | ||
C、y=±（
| ||
D、y=±（
|
设F1，F2是双曲线C：
-
=1（a＞0，b＞0）的左、右两个焦点，若双曲线C上存在点P满足|PF1|：|PF2|=2：1且∠F1PF2=90°，则双曲线C的渐近线方程是（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| A、x±2y=0 |
| B、2x±y=0 |
| C、5x±4y=0 |
| D、4x±5y=0 |