集合M={y|y=|cos2x|,x∈R},集合N={x||
|<1,i为虚数单位,x∈R},则M∩N为( )
| x |
| i |
| A、(0,1) |
| B、[0,1) |
| C、(0,1] |
| D、[0,1] |
已知函数y=f(x)的图象如图所示,则下列说法中错误的是( )
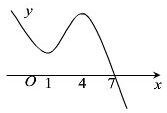

| A、f(x)在区间(-∞,1)上单调递减 |
| B、f(x)在区间(1,4)上单调递增 |
| C、当4<x<7时,f'(x)>0 |
| D、当x=1时,f'(x)=0 |
等差数列{an}的前n项和Sn满足Sn=n2,则其公差d等于( )
| A、2 | B、4 | C、±2 | D、±4 |
已知集合A={-1,0,1},B={x|x=|a+1|,a∈A},则A∩B=( )
| A、{0} | B、{1} |
| C、{0,1} | D、{0,1,2} |
已知点M(2,-3),N(-3,-2),直线ax+y-1-a=0与线段MN相交,则实数a的取值范围是( )
A、-
| ||
B、-4≤a≤
| ||
C、a≤-
| ||
D、a≤-4或a≥
|
△ABC中sin2A-sin2B-sin2C≥
sinBsinC时,角A的取值范围是( )
| 3 |
A、(0,
| ||
B、[
| ||
C、[
| ||
D、[0,
|
已知an=logn+1(n+2)(n∈N*),观察下列运算:
a1•a2=log23•log34=
•
=2;
a1•a2•a3•a4•a5•a6=log23•log34•…•log78=
•
•…•
=3;….
若a1•a2•a3•…•ak(k∈N*)为整数,则称k为“企盼数”,试确定当a1•a2•a3•…•ak=2 014时,“企盼数”k为( )
a1•a2=log23•log34=
| lg3 |
| lg2 |
| lg4 |
| lg3 |
a1•a2•a3•a4•a5•a6=log23•log34•…•log78=
| lg3 |
| lg2 |
| lg4 |
| lg3 |
| lg8 |
| lg7 |
若a1•a2•a3•…•ak(k∈N*)为整数,则称k为“企盼数”,试确定当a1•a2•a3•…•ak=2 014时,“企盼数”k为( )
| A、22014+2 |
| B、22014 |
| C、22014-2 |
| D、22014-4 |
“a,b,c为实数,如果a=b,b=c,则a=c”.类比得到下列四个命题,其中假命题为( )
| A、a,b,c为空间三条不重合的直线,如果a⊥b,b⊥c,那么a⊥c |
| B、a,b,c为空间三条不重合的直线,如果a∥b,b∥c,那么a∥c |
| C、a,b,c为实数,如果a>b,b>c,那么a>c |
| D、A,B,C为集合,如果A?B,B?C,那么A?C |
若a<b<0下列不等式中不成立的是的是( )
| A、.|a|>|b| | ||||
B、
| ||||
C、
| ||||
| D、a2>b2 |
双曲线C:
(φ为参数)的一个焦点为( )
|
| A、(3,0) |
| B、(4,0) |
| C、(5,0) |
| D、(0,5) |