题目内容
“a,b,c为实数,如果a=b,b=c,则a=c”.类比得到下列四个命题,其中假命题为( )
| A、a,b,c为空间三条不重合的直线,如果a⊥b,b⊥c,那么a⊥c |
| B、a,b,c为空间三条不重合的直线,如果a∥b,b∥c,那么a∥c |
| C、a,b,c为实数,如果a>b,b>c,那么a>c |
| D、A,B,C为集合,如果A?B,B?C,那么A?C |
考点:命题的真假判断与应用
专题:简易逻辑,推理和证明
分析:根据空间直线位置关系的定义和几何特征,可判断A,B;根据不等式的传递性,可判断C;根据集合包含关系的传递性,可判断D.
解答:
解:a,b,c为空间三条不重合的直线,如果a⊥b,b⊥c,那么a与c可能平行,可能相交,也可能异面,夹角不确定,故A错误;
a,b,c为空间三条不重合的直线,如果a∥b,b∥c,由平行公理得:a∥c,故B正确;
a,b,c为实数,如果a>b,b>c,那么a>c,故C正确;
A,B,C为集合,如果A?B,B?C,那么A?C,故D正确;
故选:A
a,b,c为空间三条不重合的直线,如果a∥b,b∥c,由平行公理得:a∥c,故B正确;
a,b,c为实数,如果a>b,b>c,那么a>c,故C正确;
A,B,C为集合,如果A?B,B?C,那么A?C,故D正确;
故选:A
点评:本题以类比推理为载体,考查了命题的真假判断与应用,难度不大,属于基础题.

练习册系列答案
相关题目
函数y=
的导数是( )
| 1 |
| (3x-1)2 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
设a,b为两条直线,α,β为两个平面,下列说法正确的是( )
| A、若a?α,b?β,a∥b,则α∥β |
| B、若a、b是两条异面直线,且a∥α、a∥β,b∥α,b∥β,则α∥β |
| C、若a∥α,b?α,则a∥b |
| D、若a∥α,b∥β,α∥β,则a∥b |
如图程序框图是古代一数学家的算法程序框图,它输出的结果S代表( )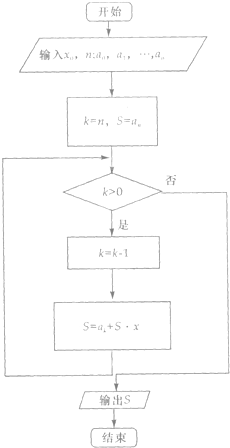

| A、一个数列的和 |
| B、一个n次多项式系数的和 |
| C、自变量取x.时,n次多项式函数的值 |
| D、自变量取x时,n个代数式的值 |
等差数列{an}的前n项和Sn满足Sn=n2,则其公差d等于( )
| A、2 | B、4 | C、±2 | D、±4 |
在△ABC中,AB=
,A=45°,B=75°,则BC=( )
| 3 |
A、
| ||
| B、2 | ||
C、3-
| ||
D、3+
|
下列程序框通常用来表示赋值、计算功能的是( )
A、. |
B、 |
C、. |
D、. |