题目内容
集合M={y|y=|cos2x|,x∈R},集合N={x||
|<1,i为虚数单位,x∈R},则M∩N为( )
| x |
| i |
| A、(0,1) |
| B、[0,1) |
| C、(0,1] |
| D、[0,1] |
考点:交集及其运算
专题:集合
分析:求出M中y的范围确定出M,求出N中x的范围确定出N,找出M与N的交集即可.
解答:
解:由M中y=|cos2x|,得到0≤y≤1,即M=[0,1];
由N中|
|<1,得到x2<1,即-1<x<1,
∴N=(-1,1),
则M∩N=[0,1).
故选:B.
由N中|
| x |
| i |
∴N=(-1,1),
则M∩N=[0,1).
故选:B.
点评:此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知正方体ABCD-A1B1C1D1,点M为线段AB的中点,点P在正方形ABCD所在平面内运动; 若PD1=3PM,则点P的轨迹为( )
| A、圆 | B、椭圆 | C、双曲线 | D、抛物线 |
如图程序框图是古代一数学家的算法程序框图,它输出的结果S代表( )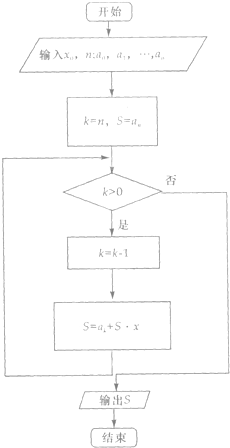

| A、一个数列的和 |
| B、一个n次多项式系数的和 |
| C、自变量取x.时,n次多项式函数的值 |
| D、自变量取x时,n个代数式的值 |
△ABC中sin2A-sin2B-sin2C≥
sinBsinC时,角A的取值范围是( )
| 3 |
A、(0,
| ||
B、[
| ||
C、[
| ||
D、[0,
|
在△ABC中,AB=
,A=45°,B=75°,则BC=( )
| 3 |
A、
| ||
| B、2 | ||
C、3-
| ||
D、3+
|
设等差数列{an}的前n项和为Sn,已知S12>0,S13<0,则S1、S2、…、S12中值最大的为( )
| A、S6 |
| B、S7 |
| C、S6或S7 |
| D、不确定 |
函数f(x)=3sinx+5sin(x+60°)的最大值是( )
| A、8 | B、7 | C、6.5 | D、5.5 |
已知△ABC中,a、b分别是角A、B所对的边,且a=x(x>0),b=2,A=60°,若三角形有两解,则x的取值范围是( )
A、x>
| ||
| B、0<x<2 | ||
C、
| ||
D、
|